【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
参考答案:
【答案】(1)1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨;
(2)共有2种租车方案:①租A型车6辆,B型车2辆;②租A型车2辆,B型车5辆;
(3)最省钱的租车方案为方案②,租车费用为800元.
【解析】
(1)根据2辆A型车和1辆B型车装满货物=10吨;1辆A型车和2辆B型车装满货物=11吨,列出方程组即可解决问题.
(2)由题意得到3a+4b=26,根据a、b均为正整数,即可求出a、b的值.
(3)求出每种方案下的租金数,经比较、分析,即可解决问题.
解:(1)设1辆A型车和1辆B型车都装满货物一次可分别运货λ吨、μ吨,
由题意得:![]() ,
,
解得:![]()
故1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨.
(2)由题意和(1)得:3a+4b=26,
∵a、b均为非负整数,
∴![]() 或
或![]() ,
,
∴共有2种租车方案:
①租A型车6辆,B型车2辆,
②租A型车2辆,B型车5辆.
(3)方案①的租金为:6×100+2×120=840(元),
方案②的租金为:2×100+5×120=800(元),
∵840>800,
∴最省钱的租车方案为方案②,租车费用为800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为x+3=2,解得x=-1;
当x+3<0时,原方程可化为x+3=-2,解得x=-5.
所以原方程的解是x=-1或x=-5.
(1)解方程:|3x-2|-4=0.
(2)已知关于x的方程|x-2|=b+1.
①若方程无解,则b的取值范围是 .
②若方程只有一个解,则b的值为 .
③若方程有两个解,则b的取值范围是 .
-
科目: 来源: 题型:
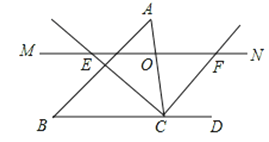
查看答案和解析>>【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价比乙种图书的单价多10元,且购买3本甲种图书和2本乙种图书共需花费130元
(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共50本,且投入总经费不超过1200元,则最多可以购买甲种图书多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,抛物线y=﹣
 x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=
x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=  PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;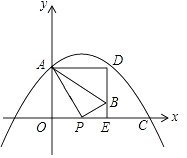
(1)求抛物线的解析式;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=
 ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

