【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

参考答案:
【答案】(1)45°;(2)DE=DF,DE⊥DF
【解析】分析:(1)根据![]() 是等腰直角三角形定义可得:
是等腰直角三角形定义可得:![]()
(2)连接CD,首先根据![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点D是AB的中点得到
,点D是AB的中点得到![]() 从而得到
从而得到![]() ≌
≌![]() ,证得
,证得![]()
详解:(1)∵△ABC是等腰直角三角形,![]()
∴![]()
故答案为:![]() ;
;
(2)DE=DF,DE⊥DF,
证明:连接CD,

∵△ABC是等腰直角三角形,∠C=![]() ,点D是AB的中点,
,点D是AB的中点,
∴CD=AD=BD,CD⊥AD,
∴![]()
∵AF=CE,
∴△DCE≌△DAF(SAS),
∴DE=DF,∠ADF=∠CDE,
∴∠ADF+∠FDC=∠CDE+∠FDC,
∵∠CDA=![]() ,
,
∴∠EDF=![]() ,
,
∴DE=DF,DE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空:
(a﹣b)(a+b)=
(a﹣b)(a2+ab+b2)=
(a﹣b)(a3+a2b+ab2+b3)=
(2)猜想:(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)= (其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:39﹣38+37﹣…+33﹣32+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx﹣4与x轴交于A,B两点,(点B在点A的右侧)且A,B两点的坐标分别为(﹣2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交BD于点M.

(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC═8,tanA═
 ,那么CF:DF═
,那么CF:DF═ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张方桌由
 个桌面和
个桌面和 条桌腿组成,如果
条桌腿组成,如果 木料可以做方桌的桌面
木料可以做方桌的桌面 个或做桌腿
个或做桌腿 条,现有
条,现有 木料,那么应需要多少立方米的木料制作桌面,多少立方米的木料制作桌腿才能使桌面和桌腿正好配套?
木料,那么应需要多少立方米的木料制作桌面,多少立方米的木料制作桌腿才能使桌面和桌腿正好配套? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,如果DE∥BC,且DE=
 BC.
BC.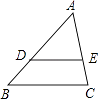
(1)如果AC=6,求CE的长;
(2)设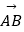 =
= 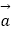 ,
, 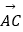 =
= 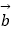 ,求向量
,求向量 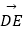 (用向量
(用向量 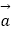 、
、 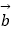 表示).
表示). -
科目: 来源: 题型:
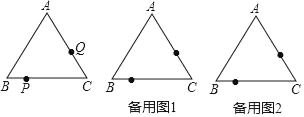
查看答案和解析>>【题目】如图,△ABC是边长为6cm的等边三角形.若点P以1cm/s的速度从点B出发,同时点Q以1.5cm/s的速度从点C出发,都按逆时针方向沿△ABC的边运动,运动时间为6秒.
(1)试求出运动到多少秒时,直线PQ与△ABC的某边平行;
(2)当运动到t1秒时,P、Q对应的点为P1、Q1,当运动到t2秒时(t1≠t2),P、Q对应的点为P2、Q2,试问:△P1CQ1与△P2CQ2能否全等?若能,求出t1、t2的值;若不能,请说明理由.
相关试题

