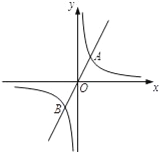
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
参考答案:
【答案】(1)k=2(2)当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1)
)、(﹣2,﹣1)或(2,1)
【解析】分析:(1)过点A作AD⊥x轴,垂足为D,由点A、B的对称性可求出OA的值,根据点在直线上,设点A的坐标为(a,2a),在Rt△OAD中,通过勾股定理即可求出A的坐标,由点A的坐标利用待定系数法即可求出结论;
(2)由点A、B的对称性,结合点A的坐标求出点B的坐标,根据点C在反比例函数上,设出点C的坐标为(n,![]() ),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
详解:(1)过点A作AD⊥x轴,垂足为D,如图1所示.
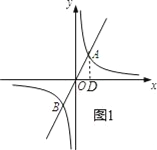
由题意可知点A与点B关于点O中心对称,且AB=2![]() ,∴OA=OB=
,∴OA=OB=![]() .
.
设点A的坐标为(a,2a),在Rt△OAD中,∠ADO=90°,由勾股定理得:
a2+(2a)2=(![]() )2,解得:a=1,∴点A的坐标为(1,2).
)2,解得:a=1,∴点A的坐标为(1,2).
把A(1,2)代入y=![]() 中得:2=
中得:2=![]() ,解得:k=2.
,解得:k=2.
(2)∵点A的坐标为(1,2),点A、B关于原点O中心对称,
∴点B的坐标为(﹣1,﹣2).设点C的坐标为(n,![]() ),
),
△ABC为直角三角形分三种情况:
①∠ABC=90°,则有AB⊥BC,![]() =﹣1,即n2+5n+4,
=﹣1,即n2+5n+4,
解得:n1=﹣4,n2=﹣1(舍去),此时点C的坐标为(﹣4,﹣![]() );
);
②∠BAC=90°,则有BA⊥AC,![]() =﹣1,即n2﹣5n+4=0,
=﹣1,即n2﹣5n+4=0,
解得:n3=4,n4=1(舍去),此时点C的坐标为(4,![]() );
);
③∠ACB=90°,则有AC⊥BC,![]() =﹣1,即n2=4,解得:n5=﹣2,n6=2,
=﹣1,即n2=4,解得:n5=﹣2,n6=2,
此时点C的坐标为(﹣2,﹣1)或(2,1).综上所述:当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1).
)、(﹣2,﹣1)或(2,1).
-
科目: 来源: 题型:
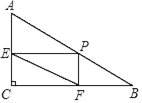
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
-
科目: 来源: 题型:
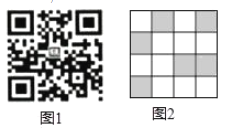
查看答案和解析>>【题目】利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系绕,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,那么表示7班学生的识别图案是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果两个角的差的绝对值等90°,就可以称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角),如图,OC⊥AB于点O,OE⊥OD,图中所有互为垂角的角有( )
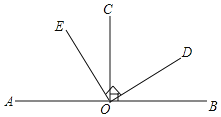
A.2对B.3对C.4对D.6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由.
(2)若AB=16,AC=12,求四边形ADCE的面积.
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE,若图中所有线段的长度之和是线段AD长度的7倍,则
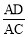 的值为( )
的值为( )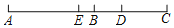
A.
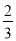 B.
B.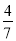 C.
C.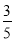 D.
D.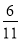
相关试题

