搜索
【题目】如图，C为线段AB延长线上一点，D为线段BC上一点，CD＝2BD，E为线段AC上一点，CE＝2AE，若图中所有线段的长度之和是线段AD长度的7倍，则
的值为( )
A.
B.
C.
D.
参考答案：
【答案】A
【解析】
设CD=2BD=2x，CE=2AE=2y，则BD=x，AE=y，再用x、y表示出所有线段的长度之和；
进而用x、y表示出AD=AE+ED的长，据此结合题意得到等式，求出x、y的关系式，然后用x表示出AD、AC，从而求出
的值.
设CD=2BD=2x，CE=2AE=2y，
则BD=x，AE=y，
∵AC=AE+EC=3y，ED=CE-CD=2y-2x，
∴所有线段的长度之和为AE+AB+AD+AC+EB+ED+EC+BD+BC+DC
=(AE+EC)+(AB+BC)+(AD+DC)+AC+(EB+BD)+ED
=4AC+2ED=43y+2(2y-2x)=12y+4y-4x=16y-4x，
又∵AD=AE+ED=y+2y-2x=3y-2x，
∴根据题意，得16y-4x=7(3y-2x)，即y=2x，
∴AD=3y-2x=4x，AC=3y=6x，
.
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正比例函数y=2x的图象与反比例函数y=
的图象交于点A、B，AB=2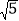
，（1）求k的值；
（2）若反比例函数y=
的图象上存在一点C，则当△ABC为直角三角形，请直接写出点C的坐标．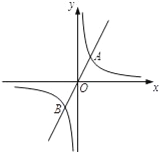
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB＝90°，D为AB的中点，四边形BCED为平行四边形，DE，AC相交于F.连接DC，AE.
（1）试确定四边形ADCE的形状，并说明理由．
（2）若AB＝16，AC＝12，求四边形ADCE的面积．
（3）当△ABC满足什么条件时，四边形ADCE为正方形？请给予证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠A＝90°，点D，E分别在AC，BC上，且CD·BC＝AC·CE，以E为圆心，DE长为半径作圆，⊙E经过点B，与AB，BC分别交于点F，G．
（1）求证：AC是⊙E的切线；
（2）若AF＝4，CG＝5，
①求⊙E的半径；
②若Rt△ABC的内切圆圆心为I，则IE＝ ．
-
科目： 来源： 题型：
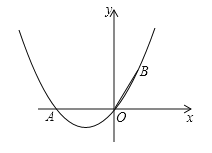
查看答案和解析>>【题目】如图，在直角坐标系中，点A的坐标为（-2，0），OB=OA，且∠AOB=120°．
（1）求经过A、O、B三点的抛物线的解析式；
（2）在（1）中抛物线的对称轴上是否存在点C，使△OBC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；
（3）若点M为抛物线上一点，点N为对称轴上一点，是否存在点M、N使得A、O、M、N构成的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛，他收集了小明、小白近期10次数学考试成绩，并绘制了折线统计图(如图所示)
项目
众数
中位数
平均数
方差
最高分
小明
85
85
小白
70，100
85
100
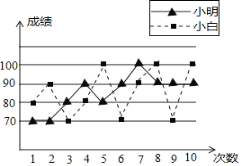
(1)根据折线统计图，张老师绘制了不完整的统计表，请你补充完整统计表；
(2)你认为张老师会选择哪位同学参加比赛？并说明你的理由
-
科目： 来源： 题型：
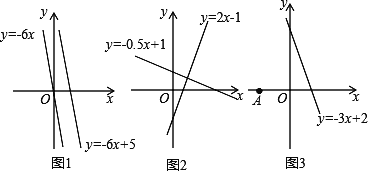
查看答案和解析>>【题目】材料一：如图1，由课本91页例2画函数y＝﹣6x与y＝﹣6x+5可知，直线y＝﹣6x+5可以由直线y＝﹣6x向上平移5个单位长度得到由此我们得到正确的结论一：在直线L1：y=K1x+b1与直线L2：y=K2x+b2中，如果K1=K2 且b1≠b2 ，那么L1∥L2，反过来，也成立．
材料二：如图2，由课本92页例3画函数y＝2x﹣1与y＝﹣0.5x+1可知，利用所学知识一定能证出这两条直线是互相垂直的．由此我们得到正确的结论二：在直线L1：y=k1x+b1 与L2：y=k2x+b2 中，如果k1·k2=-1那么L1⊥L2，反过来，也成立
应用举例
已知直线y＝﹣
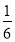x+5与直线y＝kx+2互相垂直，则﹣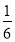k＝﹣1．所以k＝6解决问题
(1)请写出一条直线解析式______，使它与直线y＝x﹣3平行．
(2)如图3，点A坐标为(﹣1，0)，点P是直线y＝﹣3x+2上一动点，当点P运动到何位置时，线段PA的长度最小？并求出此时点P的坐标．
相关试题
