【题目】如图,矩形ABCD中,AB=1,AD=2,E是AD中点,P在射线BD上运动,若△BEP为等腰三角形,则线段BP的长度等于 . 
参考答案:
【答案】![]() 或
或 ![]() 或
或 ![]()
【解析】解:∵矩形ABCD中,AB=1,AD=2,E是AD中点, ∴∠BAD=90°,AE=DE=1,
∴△ABE是等腰直角三角形,
∴BE= ![]() AB=
AB= ![]() .
.
若△BEP为等腰三角形,则分三种情况:①当BP=BE时,显然BP= ![]() ;②当PB=PE时,如图,连结AP.
;②当PB=PE时,如图,连结AP.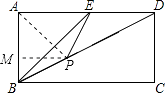
∵PB=PE,AB=AE,
∴AP垂直平分BE,
∵△ABE是等腰直角三角形,
∴∠BAP=∠EAP=45°.
作PM⊥AB于M,设PM=x,
∵S△ABD=S△ABP+S△APD
∴ ![]() ×1x+
×1x+ ![]() ×2x=
×2x= ![]() ×1×2,
×1×2,
解得x= ![]() ,
,
∴PM= ![]() ,
,
∴BP= ![]() =
= ![]() =
= ![]() ;③当EB=EP时,如图,过A作AF⊥BD于F,
;③当EB=EP时,如图,过A作AF⊥BD于F,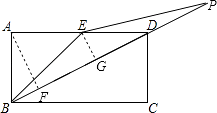
过E作EG⊥BD于G.
在Rt△ABF中,AF=ABsin∠ABF=1× ![]() =
= ![]() ,
,
∵AE=ED,EG∥AF,
∴EG= ![]() AF=
AF= ![]() .
.
在Rt△BEG中,∵BE= ![]() ,EG=
,EG= ![]() ,
,
∴BG= ![]() =
= ![]() .
.
∵EB=EP,EG⊥BP,
∴BP=2BG= ![]() .
.
综上所述,线段BP的长度等于 ![]() 或
或 ![]() 或
或 ![]() .
.
故答案为 ![]() 或
或 ![]() 或
或 ![]() .
.
先根据矩形的性质及中点的定义得出∠BAD=90°,AE=DE=1,那么△ABE是等腰直角三角形,BE= ![]() AB=
AB= ![]() .再分三种情况讨论:①BP=BE;②PB=PE;③EB=EP.
.再分三种情况讨论:①BP=BE;②PB=PE;③EB=EP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程mx2+(2m﹣1)x+m=0有两个不相等的实数根,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图像经过点(-2,4),且与正比例函数y=2x的图像平行.
(1) 求一次函数y=kx+b的解析式;
(2) 求一次函数y=kx+b的图像与坐标轴所围成的三角形的面积;
(3) 若A(a,y1),B(a+b,y2)为一次函数y=kx+b的图像上两个点,试比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在
 处,
处,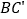 交AD于点E.
交AD于点E.(1)试判断△BDE的形状,并说明理由;
(2)若
 ,
, ,求△BDE的面积.
,求△BDE的面积.
相关试题

