搜索
【题目】如图，填空:
(1)若∠4=∠3，则____∥_____，理由是______；
(2)若∠2=∠E，则____∥___，理由是____；
(3)若∠A=∠ABE=180°，则____∥___，理由是____；
(4)若∠2=∠____，则DA∥EB，理由是____；
(5)若∠DBC+∠_____=180°，则DB∥EC，理由是____；
参考答案：
【答案】AD, BE, 同位角相等，两直线平行, BD, CE, 内错角相等，两直线平行, AD, BE, 同旁内角互补，两直线平行, D, 内错角相等,两直线平行, C, 同旁内角互补，两直线平行
【解析】
根据平行线的判定方法解答即可.
(1)若∠4=∠3，则_AD__∥__BE__，理由是；(同位角相等，两直线平行);
(2)若∠2=∠E，则__BD__∥_CE__，理由是(内错角相等，两直线平行)；
(3)若∠A=∠ABE=180°，则_AD___∥__BE_，理由是(同旁内角互补，两直线平行)；
(4)若∠2=∠_D___，则DA∥EB，理由是(内错角相等,两直线平行)；
(5)若∠DBC+∠_C_=180°，则DB∥EC，理由是(同旁内角互补，两直线平行)；
故答案为：(1). AD (2). BE (3). 同位角相等，两直线平行； (4). BD， (5)CE, (6)内错角相等，两直线平行; (7). AD, (8)BE, (9)同旁内角互补，两直线平行； (10). D (11). 内错角相等,两直线平行; (12).C, (13) 同旁内角互补，两直线平行.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．
（1）求证：AB=CD；
（2）若AB=CF，∠B=30°，求∠D的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=1，AD=2，E是AD中点，P在射线BD上运动，若△BEP为等腰三角形，则线段BP的长度等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y＝kx＋b的图像经过点(－2，4)，且与正比例函数y＝2x的图像平行．
(1) 求一次函数y＝kx＋b的解析式；
(2) 求一次函数y＝kx＋b的图像与坐标轴所围成的三角形的面积；
(3) 若A(a，y1)，B(a＋b，y2)为一次函数y＝kx＋b的图像上两个点，试比较y1与y2的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将长方形ABCD沿着对角线BD折叠，使点C落在
处，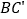
交AD于点E．（1）试判断△BDE的形状，并说明理由；
（2）若
，
，求△BDE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB、BC、AC三边的长分别为
， 
， 
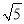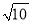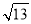，求这个三角形的面积．小明同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．（1）△ABC的面积为 ．
（2）若△DEF的三边DE、EF、DF长分别为
， 
， 
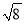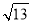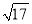，请在图2的正方形网格中画出相应的△DEF，并求出△DEF的面积为 ．（3）在△ABC中，AB=2
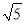，AC=4，BC=2，以AB为边向△ABC外作△ABD（D与C在AB异侧），使△ABD为等腰直角三角形，则线段CD的长为 ．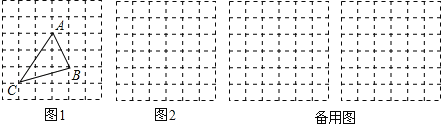
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
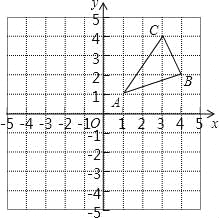
（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
（2）请画出△ABC关于原点对称的△A2B2C2；
（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．
相关试题
