【题目】如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE交AD 于点 F.
(1)求证:△BDF 是等腰三角形;
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;

②若 AD=AB+2,BD=10,求四边形 BFDG 的面积.
参考答案:
【答案】(1)证明见解析;(2)①四边形BFDG是菱形;理由见解析;②![]() .
.
【解析】
(1)根据折叠的性质可得∠DBC=∠DBE,根据矩形的性质可得∠DBC=∠ADB,等量代换可得∠DBE=∠ADB,问题得证;
(2)①根据矩形的性质及第一问证得邻边相等可得四边形BFDG是菱形;
②在△ABD中根据勾股定理列一元二次方程求出AB,然后在直角△ABF中设DF=BF=x,利用勾股定理构造方程求解,最后根据菱形面积公式计算即可.
解:(1)证明:如图1,
根据折叠的性质可得:∠DBC=∠DBE,
∵AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①∵四边形ABCD是矩形,
∴AD∥BC,
又∵DG∥BE,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;

②由勾股定理得:AB2+AD2=BD2,即AB2+(AB+2)2=100,
解得:AB=6(负值已舍去),
∴AD=AB+2=8,
设DF=BF=x,则AF=ADDF=8x.
在直角△ABF中,AB2+AF2=BF2,即62+(8x)2=x2,
解得x=![]() ,
,
∴S四边形 BFDG=![]() .
.
-
科目: 来源: 题型:
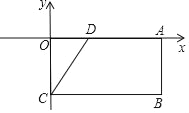
查看答案和解析>>【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
(1)求过点B、C、D的抛物线的解析式;
(2)求出(1)中抛物线与x轴的另一个交点E坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第
 个格子的数为_____.
个格子的数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,∠C=90°,DC=5,以CD为半径的⊙C与以AB为半径的⊙B相交于点E、F,且点E在BD上,联结EF交BC于点G.
(1)设BC与⊙C相交于点M,当BM=AD时,求⊙B的半径;
(2)设BC=x,EF=y,求y关于x的函数关系式,并写出它的定义域;
(3)当BC=10时,点P为平面内一点,若⊙P与⊙C相交于点D、E,且以A、E、P、D为顶点的四边形是梯形,请直接写出⊙P的面积.(结果保留π)

-
科目: 来源: 题型:
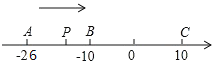
查看答案和解析>>【题目】已知数轴上有A、B、C三点,分别表示有理数﹣26,﹣10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒。
(1)用含t的代数式表示P到点A和点C的距离:PA=_____,PC=_____.
(2)当点P运动到B点时,点Q从A出发,以每秒3个单位的速度向右运动,求t等于多少秒时P、Q两点相遇?t等于多少秒时P、Q两点相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月19日下午,安徽省政府在安徽省政务服务中心召开新闻发布会,发布2017年全省经济运行情况.2017年全省生产总值27518.7亿元,按可比价格计算,比上年增长8.5%.将27518.7亿元用科学记数法表示是( )
A. 2.75187×104 B. 2.75187×1011 C. 2.75187×1012 D. 2.75187×1013
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列各题并按要求完成:
(1)定义:若两个一元二次方程有一个相同的实数根,则称这两个方程为“友好方程”,已知关于x的一元二次方程 x 2x 0 与 x 3x m 1 0 为“友好方程”,求 m 的值;
(2)关于x的一元二次方程
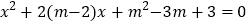 有两个不相等的实数根
有两个不相等的实数根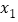 ,
,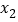 ,且二次根式
,且二次根式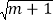 有意义,若T=
有意义,若T=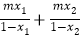 ,求T的取值范围;
,求T的取值范围;(3)我们不妨约定方程的整数解称之为“硬核”,例如x=1就称为方程(x-1)(2x+1)=0 的一个“硬核”,若一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0(k为常数)有两个不同的“硬核”,试确定方程的两个“硬核”及常数 k 的值.
相关试题

