【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
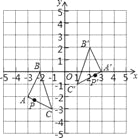
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
参考答案:
【答案】
【解析】
试题本题考查了坐标与图形变化,解决本题的关键是根据已知对应点找到各对应点之间的变化规律. 根据已知三对对应点的坐标,得出变换规律,再让点P的坐标也做相应变化即可.
解:∵A(﹣3,﹣2),B(﹣2,0),C(﹣1,﹣3),
A′(3,0),B′(2,2),C′(1,﹣1),
∴横坐标互为相反数;纵坐标增加了0﹣(﹣2)=2﹣0=﹣1﹣(﹣3)=2;
∵△ABC边上点P的坐标为(a,b),
∴点P变换后的对应点P′的坐标为(﹣a,b+2).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内有两点
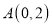 、
、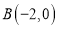 ,且
,且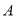 、
、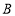 两点之间的距离等于
两点之间的距离等于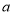 (
(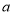 为大于0的已知数),在不计算
为大于0的已知数),在不计算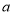 的数值条件下,完成下列两题:
的数值条件下,完成下列两题: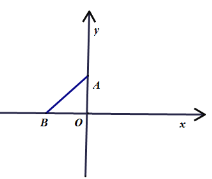
(1)以学过的知识用一句话说出
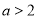 的理由;
的理由;(2)在
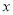 轴上是否存在点
轴上是否存在点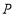 ,使
,使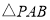 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点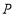 的坐标,并求
的坐标,并求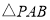 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
问题背景
在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:
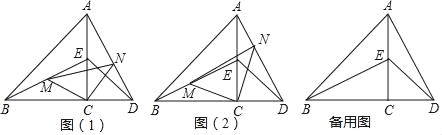
如图,点C在线段BD上,点E在线段AC上.∠ACB=∠ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.
“兴趣小组”写出的两个教学结论是:①△BCE≌△ACD;②当CM,CN分别是△BCE和△ACD的中线时,△MCN是等腰直角三角形.
解决问题
(1)请你结合图(1).证明“兴趣小组”所写的两个结论的正确性.
类比探究
受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图(2),当∠BCM=∠ACN时,△MCN是等腰直角三角形.
(2)“实践小组”所写的结论是否正确?请说明理由.
感悟发现
“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,△MCN仍然是等腰直角三角形请你思考:
(3)“奋进小组”所提结论是否正确?答: (填“正确”、“不正确”或“不一定正确”.)
(4)反思上面的探究过程,请你添加适当的条作,再写出使得△MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市先后两次共进货板栗
 ,进货价依次为10元
,进货价依次为10元 和8元
和8元 ,且第二次比第一次多付款800元.
,且第二次比第一次多付款800元.(1)该超市这两次购进的板栗分别是多少吨?
(2)超市对这
 板栗以14元
板栗以14元 的标价销售了
的标价销售了 后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.

(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
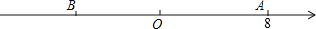
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
-
科目: 来源: 题型:
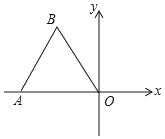
查看答案和解析>>【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以点O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,画出△OA′B′,写出点A′,B′的坐标.
相关试题

