【题目】如图,在直角坐标平面内有两点![]() 、
、![]() ,且
,且![]() 、
、![]() 两点之间的距离等于
两点之间的距离等于![]() (
(![]() 为大于0的已知数),在不计算
为大于0的已知数),在不计算![]() 的数值条件下,完成下列两题:
的数值条件下,完成下列两题:
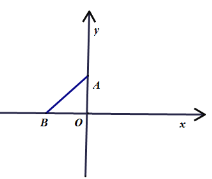
(1)以学过的知识用一句话说出![]() 的理由;
的理由;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点![]() 的坐标,并求
的坐标,并求![]() 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由.
参考答案:
【答案】(1)垂线段最短;(2)存在,当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() .
.
【解析】
(1)利用垂线段最短即可得出结论;
(2)分类讨论,利用等腰三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,
∵![]() ,
,
∴![]() ,
,
∵垂线段最短,且![]() 不与O重合,
不与O重合,
∴![]() ,即
,即![]() ,
,
∴![]() 的理由是“垂线段最短”;
的理由是“垂线段最短”;
(2)在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
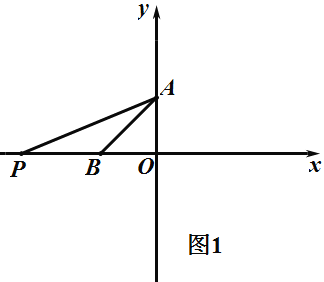
②如图2,当P在B点右边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
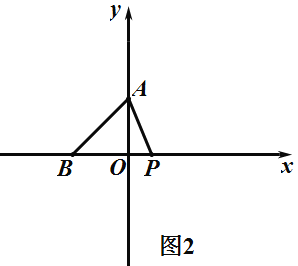
③如图3,当P在B点右边,BP=AP,![]() 为等腰三角形,
为等腰三角形,
此时P与O重合,即![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
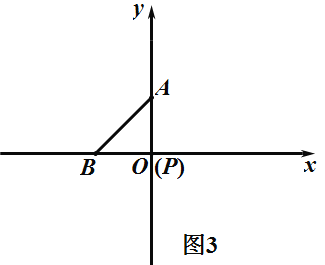
④如图4,当P在B点右边,AP=AB=a,![]() 为等腰三角形,
为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;

综上所述:在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技与经济的发展,机器人自动化线的市场越来越大,并且逐渐成为自动化生产线的主要方式某化工厂要在规定时间内搬运1800千克化工原料,现有A,B两种机器人可供选择,已知A型机器人每小时完成的工作量是B型机器人的1.5倍,A型机器人单独完成所需的时间比B型机器人少10小时.
(1)求两种机器人每小时分别搬运多少千克化工原料?
(2)若A型机器人工作1小时所需的费用为80元,B型机器人工作1小时所需的费用为60元,若该工厂在两种机器人中选择其中的一种机器人单独完成搬运任务,则选择哪种机器人所需费用较小?请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯
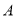 射线从
射线从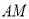 开始顺时针旋转至
开始顺时针旋转至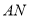 便立即回转,灯
便立即回转,灯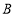 射线从
射线从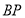 开始顺时针旋转至
开始顺时针旋转至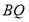 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯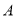 转动的速度是每秒2度,灯
转动的速度是每秒2度,灯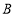 转动的速度是每秒1度.假定主道路是平行的,即
转动的速度是每秒1度.假定主道路是平行的,即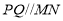 ,且
,且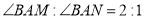 .
.(1)填空:
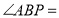 ______
______ ;
;(2)若灯
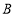 射线先转动60秒,灯
射线先转动60秒,灯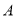 射线才开始转动,在灯
射线才开始转动,在灯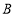 射线到达
射线到达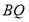 之前,
之前,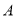 灯转动几秒,两灯的光束互相平行?
灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯
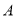 射线到达
射线到达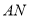 之前,若射出的光束交于点
之前,若射出的光束交于点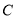 ,过
,过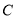 作
作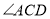 交
交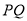 于点
于点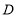 ,且
,且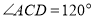 ,则在转动过程中,请探究
,则在转动过程中,请探究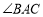 与
与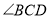 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.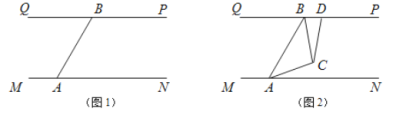
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则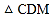 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
问题背景
在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:
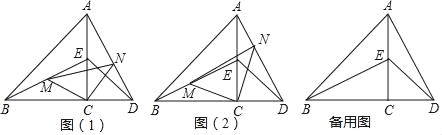
如图,点C在线段BD上,点E在线段AC上.∠ACB=∠ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.
“兴趣小组”写出的两个教学结论是:①△BCE≌△ACD;②当CM,CN分别是△BCE和△ACD的中线时,△MCN是等腰直角三角形.
解决问题
(1)请你结合图(1).证明“兴趣小组”所写的两个结论的正确性.
类比探究
受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图(2),当∠BCM=∠ACN时,△MCN是等腰直角三角形.
(2)“实践小组”所写的结论是否正确?请说明理由.
感悟发现
“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,△MCN仍然是等腰直角三角形请你思考:
(3)“奋进小组”所提结论是否正确?答: (填“正确”、“不正确”或“不一定正确”.)
(4)反思上面的探究过程,请你添加适当的条作,再写出使得△MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市先后两次共进货板栗
 ,进货价依次为10元
,进货价依次为10元 和8元
和8元 ,且第二次比第一次多付款800元.
,且第二次比第一次多付款800元.(1)该超市这两次购进的板栗分别是多少吨?
(2)超市对这
 板栗以14元
板栗以14元 的标价销售了
的标价销售了 后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本)
后,把剩下的板栗全部打折售出,合计获得利润4570元,问超市对剩下的板栗打几折销售?(利润=销售总收入-进货总成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
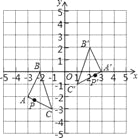
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
相关试题

