【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
参考答案:
【答案】(1)0.52,0.50,0.51, 0.50;(2)P≈0.5;
【解析】试题分析:(1)用投中的次数除以投篮的次数即可得出答案;
(2)计算出所有投篮的次数,再计算出总的命中数,继而可估计出这名球员投篮一次,投中的概率.
试题解析:(1)根据题意得:
78÷150=0.52;
104÷209≈0.50;
152÷300≈0.51;
175÷350≈0.58;
填表如下:
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 | 0.52 | 0.50 | 0.49 | 0.51 | 0.58 |
故答案为:0.52,0.50,0.51,0.58;
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720,
故这名球员投篮一次,投中的概率约为: ![]() ≈0.5.
≈0.5.
故答案为:0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗
 已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.
已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元. 、B两种树苗的单价分别是多少元?
、B两种树苗的单价分别是多少元? 该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵.
该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
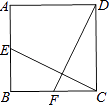
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,直线
,直线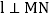 ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且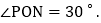 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,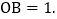 点C在直线PQ上运动
点C在直线PQ上运动 连接BC过点C作
连接BC过点C作 ,交直线MN于点A,连接
,交直线MN于点A,连接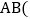 点A、C与点O都不重合
点A、C与点O都不重合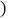 .
. 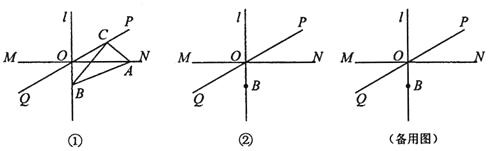
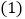 小明经过画图、度量发现:在
小明经过画图、度量发现:在 中,始终有一个角与
中,始终有一个角与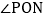 相等,这个角是________________;
相等,这个角是________________;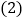 当
当 时,在图
时,在图 中画出示意图并证明
中画出示意图并证明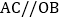 ;
;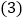 探索
探索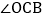 和
和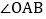 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点A(x1 , y1)和点B(x2 , y2)是反比例函数y=
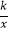 图象上的两点,当x1<x2<0时,y1>y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
图象上的两点,当x1<x2<0时,y1>y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,∠BAC=10°,P是
 的中点,则∠PAB的大小是( )
的中点,则∠PAB的大小是( ) 
A.35°
B.40°
C.60°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“6·26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:


(1)表中
 =___,
=___,  =____,并补全直方图;
=____,并补全直方图;(2)若用扇形统计图描述此成绩统计分布情况,则分数段80≤
 <100对应扇形的圆心角度数是___;
<100对应扇形的圆心角度数是___;(3)请估计该年级分数在60≤
 <70的学生有多少人?
<70的学生有多少人?
相关试题

