【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗![]() 已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.
已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.
![]() 、B两种树苗的单价分别是多少元?
、B两种树苗的单价分别是多少元?
![]() 该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵.
该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵.
参考答案:
【答案】(1)A种树苗单价为60元,B中树苗单为50元;(2)最多可以购进A种树苗15棵.
【解析】(1)设购进A种树苗每棵需要x元,B种树苗每棵需要y元,根据“2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种树苗m棵,则购进B种树苗(28-m)棵,根据总价=单价×购进数量结合总费用不超过1550元,即可得出关于m的一元一次不等式,解之即可得出结论;
![]() 设A种树苗单价为x元,B种树苗单价为y元,
设A种树苗单价为x元,B种树苗单价为y元,
根据题意,得![]() ,
,
解方程组,得![]() ,
,
答:A种树苗单价为60元,B中树苗单为50元.
![]() 设购进A种树苗m棵,则购进B种树苗
设购进A种树苗m棵,则购进B种树苗![]() 棵,
棵,
根据题意,得![]() ,
,
解不等式,得![]() ,
,
因为m为整数,所以m的最大值是15,
答:最多可以购进A种树苗15棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系
在平面直角坐标系 中的位置如图所示.
中的位置如图所示.(1)作
 关于点
关于点 成中心对称的
成中心对称的 .
.(2)将
 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的 .
.(3)在
 轴上求作一点
轴上求作一点 ,使
,使 的值最小
的值最小 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,OF平分∠AOE,∠1=15°,则下列结论中不正确的是( )
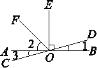
A. ∠2=45° B. ∠1=∠3 C. ∠EOD与∠3互为余角 D. ∠FOD=110°
-
科目: 来源: 题型:
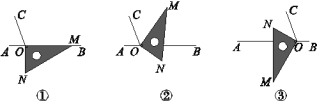
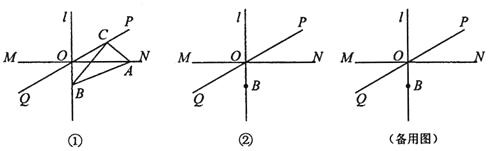
查看答案和解析>>【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
-
科目: 来源: 题型:
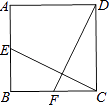
查看答案和解析>>【题目】如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,直线
,直线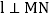 ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且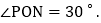 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,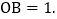 点C在直线PQ上运动
点C在直线PQ上运动 连接BC过点C作
连接BC过点C作 ,交直线MN于点A,连接
,交直线MN于点A,连接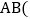 点A、C与点O都不重合
点A、C与点O都不重合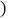 .
. 
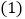 小明经过画图、度量发现:在
小明经过画图、度量发现:在 中,始终有一个角与
中,始终有一个角与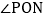 相等,这个角是________________;
相等,这个角是________________;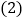 当
当 时,在图
时,在图 中画出示意图并证明
中画出示意图并证明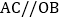 ;
;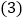 探索
探索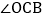 和
和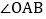 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n)
50
100
150
209
250
300
350
投中次数(m)
28
60
78
104
123
152
175
投中频率(n/m)
0.56
0.60
0.49
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
相关试题

