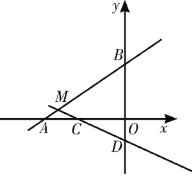
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=![]() x+4交x轴于点A,交y轴于点B.直线CD:y=-
x+4交x轴于点A,交y轴于点B.直线CD:y=-![]() x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标.
(2)若点P是射线MD的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系,并指出x的取值范围.
(3)当S=10时,平面直角坐标系内是否存在点E,使以点B,E,P,M为顶点的四边形是平行四边形?若存在,共有几个这样的点?请求出其中一个点的坐标(写出求解过程);若不存在,请说明理由.
参考答案:
【答案】(1)B(0,4),D(0,-1);(2)![]() (
(![]() );(3)存在,共有3个,E点为(4,
);(3)存在,共有3个,E点为(4,![]() )、(-6,-4)和
)、(-6,-4)和![]()
【解析】
(1)利用y轴上的点的坐标特征即可得出结论.
(2)先求出点M的坐标,再用三角形的面积之和即可得出结论.
(3)分三种情况,根据题意只写出其中一个求解过程即可,利用对角线互相平分的四边形是平行四边形和线段的中点坐标的确定方法即可得出结论.
(1)将x=0代入y=![]() x+4,y=
x+4,y=![]()
![]() +4
+4
解得![]()
将y=0代入y=-![]() x-1,y=-
x-1,y=-![]()
![]() -1
-1
解得![]()
∴B(0,4),D(0,-1)
(2)在解方程组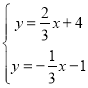
得M点的坐标是![]() ,
,
∵BD=5,
当P点在![]() 轴左侧时,如图(1):
轴左侧时,如图(1):![]() ;
;
当P点在![]() 轴右侧时,如图(2):
轴右侧时,如图(2):![]() .
.
总之,所求的函数关系式是![]() (
(![]() )
)

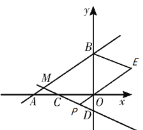
(3)存在,共有3个.
当S=10时,求得P点为(-1,![]() ),若平行四边形以MB、MP为邻边,如图,BE∥MD,PE∥MB,可设直线BE的解析式为
),若平行四边形以MB、MP为邻边,如图,BE∥MD,PE∥MB,可设直线BE的解析式为![]() ,将B点坐标代入得
,将B点坐标代入得![]() ,所以BE的解析式为
,所以BE的解析式为![]() ;同样可求得PE的解析式为
;同样可求得PE的解析式为![]() ,解方程组
,解方程组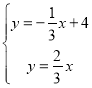
得E点为(4,![]() )
)
[{备注:同理可证另外两个点,另两个点的坐标为(-6,-4)和![]() }
}
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目
频数
频率
语文
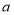
0.5
数学
12
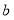
英语
6
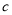
物理
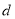
0.2
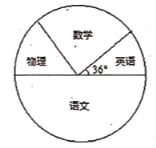
(1)求出这次调查的总人数;
(2)求出表中
 的值;
的值;(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
-
科目: 来源: 题型:
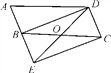
查看答案和解析>>【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
 交
交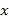 轴于点
轴于点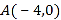 、
、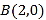 ,交
,交 轴于点
轴于点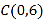 ,在
,在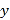 轴上有一点
轴上有一点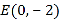 ,连接
,连接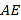 .
.
(1)求二次函数的表达式;
(2)若点
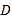 为抛物线在
为抛物线在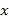 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求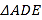 面积的最大值;
面积的最大值;(3)抛物线对称轴上是否存在点
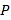 ,使
,使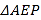 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由. -
科目: 来源: 题型:
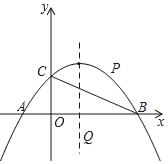
查看答案和解析>>【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
-
科目: 来源: 题型:
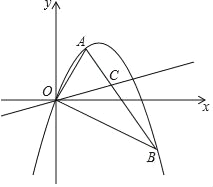
查看答案和解析>>【题目】如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,
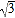 ),点B(3,﹣
),点B(3,﹣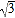 ),O为坐标原点.
),O为坐标原点.(1)求这条抛物线所对应的函数表达式;
(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;
(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,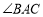 、
、 的角平分线相交于点
的角平分线相交于点 ,①若
,①若 ,则
,则 __________,②若
__________,②若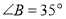 ,
, ,则
,则 ___________.
___________.
相关试题

