【题目】如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣ ![]() x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=
x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC= ![]() AB,反比例函数y=
AB,反比例函数y= ![]() 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 . 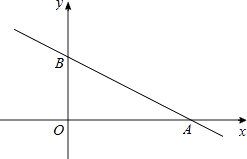
参考答案:
【答案】![]() 或﹣
或﹣ ![]()
【解析】解:在y=﹣ ![]() x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
x+1中,令y=0,则x=2;令x=0,得y=1, ∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB= ![]() .
.
设∠BAO=θ,则sinθ= ![]() ,cosθ=
,cosθ= ![]() .
.
当点C为线段AB中点时,有OC= ![]() AB,
AB,
∵A(2,0),B(0,1),
∴C(1, ![]() ).
).
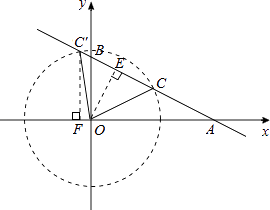
以点O为圆心,OC长为半径作圆,与直线AB的另外一个交点是C′,则点C、点C′均符合条件.
如图,过点O作OE⊥AB于点E,则AE=OAcosθ=2× ![]() =
= ![]() ,
,
∴EC=AE﹣AC= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∵OC=OC′,∴EC′=EC= ![]() ,∴AC′=AE+EC′=
,∴AC′=AE+EC′= ![]() +
+ ![]() =
= ![]() .
.
过点C′作CF⊥x轴于点F,则C′F=AC′sinθ= ![]() ×
× ![]() =
= ![]() ,
,
AF=AC′cosθ= ![]() ×
× ![]() =
= ![]() ,
,
∴OF=AF﹣OA= ![]() ﹣2=
﹣2= ![]() .
.
∴C′(﹣ ![]() ,
, ![]() ).
).
∵反比例函数y= ![]() 的图象经过点C或C′,1×
的图象经过点C或C′,1× ![]() =
= ![]() ,﹣
,﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() ,
,
∴k= ![]() 或﹣
或﹣ ![]() .
.
解法二:设C(m,﹣ ![]() m+1),
m+1),
根据勾股定理,m2+(﹣ ![]() m+1)2=(
m+1)2=( ![]()
![]() )2 ,
)2 ,
解得:m=﹣ ![]() 或1.
或1.
∴k= ![]() 或﹣
或﹣ ![]() .
.
所以答案是: ![]() 或﹣
或﹣ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)= , d(10﹣2)=;
(2)劳格数有如下运算性质: 若m、n为正数,则d(mn)=d(m)+d(n),d( )=d(m)﹣d(n).
)=d(m)﹣d(n).
根据运算性质,填空: =(a为正数),若d(2)=0.3010,则d(4)= , d(5)= , d(0.08)=;
=(a为正数),若d(2)=0.3010,则d(4)= , d(5)= , d(0.08)=;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.x
1.5
3
5
6
8
9
12
27
d(x)
3a﹣b+c
2a﹣b
a+c
1+a﹣b﹣c
3﹣3a﹣3c
4a﹣2b
3﹣b﹣2c
6a﹣3b
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(1,2),B(0,4).
(1)求此函数的解析式.
(2)求原点到直线AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为cm2 .
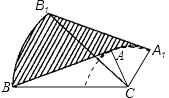
-
科目: 来源: 题型:
查看答案和解析>>【题目】市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随机调查了该校部分学生闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答下列问题:

(1)本次共调查了多少名学生?
(2)如果该校共有1500名学生,请你估计该校经常闯红灯的学生大约有多少人;
(3)针对图中反映的信息谈谈你的认识.(不超过30个字) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张长9cm,宽3cm的矩形纸片,如图所示,把它折叠使D点与B点重合,你能求出EF的长吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
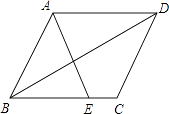
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
相关试题

