【题目】如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)= , d(10﹣2)=;
(2)劳格数有如下运算性质: 若m、n为正数,则d(mn)=d(m)+d(n),d( ![]() )=d(m)﹣d(n).
)=d(m)﹣d(n).
根据运算性质,填空:![]() =(a为正数),若d(2)=0.3010,则d(4)= , d(5)= , d(0.08)=;
=(a为正数),若d(2)=0.3010,则d(4)= , d(5)= , d(0.08)=;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
d(x) | 3a﹣b+c | 2a﹣b | a+c | 1+a﹣b﹣c | 3﹣3a﹣3c | 4a﹣2b | 3﹣b﹣2c | 6a﹣3b |
参考答案:
【答案】
(1)1;﹣2
(2)3;0.6020;0.6990;﹣1.0970
(3)解:若d(3)≠2a﹣b,则d(9)=2d(3)≠4a﹣2b,
d(27)=3d(3)≠6a﹣3b,
从而表中有三个劳格数是错误的,与题设矛盾,
∴d(3)=2a﹣b,
若d(5)≠a+c,则d(2)=1﹣d(5)≠1﹣a﹣c,
∴d(8)=3d(2)≠3﹣3a﹣3c,
d(6)=d(3)+d(2)≠1+a﹣b﹣c,
表中也有三个劳格数是错误的,与题设矛盾.
∴d(5)=a+c.
∴表中只有d(1.5)和d(12)的值是错误的,应纠正为:
d(1.5)=d(3)+d(5)﹣1=3a﹣b+c﹣1,
d(12)=d(3)+2d(2)=2﹣b﹣2c.
【解析】解:(1)d(10)=1,d(10﹣2)=﹣2; 故答案为:1,﹣2;
2) ![]() =
= ![]() =3;
=3;
因为d(2)=0.3010
故d(4)=d(2)+d(2)=0.6020,
d(5)=d(10)﹣d(2)=1﹣0.3010=0.6990,
d(0.08)=d(8×10﹣2)=3d(2)+d(10﹣2)=﹣1.0970;
(1)根据定义可知,d(10)和d(10﹣2)就是指10的指数,据此即可求解;(2)根据d(a3)=d(aaa)=d(a)+d(a)+d(a)即可求得 ![]() 的值;(3)通过9=32 , 27=33 , 可以判断d(3)是否正确,同理以依据5=10÷2,假设d(5)正确,可以求得d(2)的值,即可通过d(8),d(12)作出判断.
的值;(3)通过9=32 , 27=33 , 可以判断d(3)是否正确,同理以依据5=10÷2,假设d(5)正确,可以求得d(2)的值,即可通过d(8),d(12)作出判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣2x﹣8交y轴于点A,交x轴正半轴于点B.
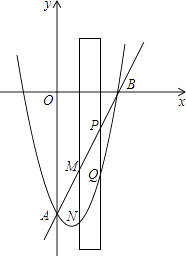
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于y轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.

(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
-
科目: 来源: 题型:
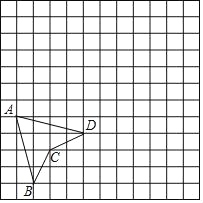
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长为1,四边形ABCD的顶点都在格点上.
(1)在方格纸上建立平面直角坐标系,使四边形ABCD的顶点A,C的坐标分别为(﹣5,﹣1),(﹣3,﹣3),并写出点D的坐标;
(2)在(1)中所建坐标系中,画出四边形ABCD关于x轴的对称图形A1B1C1D1,并写出点B的对应点B1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(1,2),B(0,4).
(1)求此函数的解析式.
(2)求原点到直线AB的距离.
-
科目: 来源: 题型:
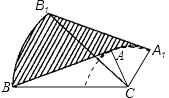
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以点O为原点的平面直角坐标系中,一次函数y=﹣
 x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=
x+1的图象与x轴交于点A,与y轴交于点B,点C在直线AB上,且OC=  AB,反比例函数y=
AB,反比例函数y= 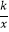 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 . 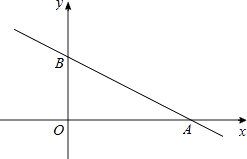
相关试题

