【题目】小明每天早上要在7:50之前赶到距家900米的学校上学.小明以60米/分的速度出发10分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以160米/分的速度去追小明,爸爸能否在小明进学校前追上他?若能,请说明理由,若不能,请计算,爸爸的速度至少为多少时才能赶在小明进学校前追上他?
参考答案:
【答案】不能,理由见解析,![]() 米/分
米/分
【解析】
设小明爸爸追上小明用了![]() 分钟,由题意知小明比爸爸多走
分钟,由题意知小明比爸爸多走![]() 分钟且找出等量关系,小明和他爸爸走的路程一样,由此等量关系列出方程求解;通过计算,爸爸按这个速度追赶,小明爸爸不能在小明进学校前追上小明;求出小明走完全程的时间,继而求得爸爸赶在小明进学校前追上他所需的最小时间,最后求得答案.
分钟且找出等量关系,小明和他爸爸走的路程一样,由此等量关系列出方程求解;通过计算,爸爸按这个速度追赶,小明爸爸不能在小明进学校前追上小明;求出小明走完全程的时间,继而求得爸爸赶在小明进学校前追上他所需的最小时间,最后求得答案.
先设小明爸爸追上小明用了![]() 分钟,那么小明走了
分钟,那么小明走了![]() 分钟,
分钟,
由题意得:![]() ,
,
解得:![]() ,
,
小明此时已经行走的路程为:![]() 米,
米,
所以,小明爸爸不能在小明进学校前追上小明.
小明走完全程需要时间为:![]() 分钟,
分钟,
∴小明爸爸在学校前追上小明速度至少为:![]() 米/分.
米/分.
∴爸爸的速度至少为180米/分才能赶在小明进学校前追上他.
-
科目: 来源: 题型:
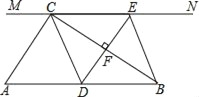
查看答案和解析>>【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形
 绕点A顺时针旋转45°得到正方形
绕点A顺时针旋转45°得到正方形 ,边
,边 与
与 交于点O,则四边形
交于点O,则四边形 的周长是( )
的周长是( )
A. 6B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
-
科目: 来源: 题型:
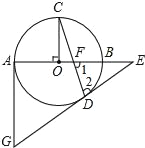
查看答案和解析>>【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形
(1)
(2)
(3)
……
黑色瓷砖的块数
4
……
黑白两种瓷砖的总块数
15
……
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数
 的图象与
的图象与 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于
 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
相关试题

