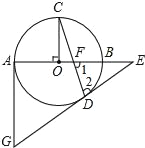
【题目】如图的⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，并与AB延长线交于点E．

（1）求证：∠1=∠2．

（2）已知：OF：OB=1：3，⊙O的半径为3，求AG的长．

参考答案：

【答案】（1）证明见解析（2）6

【解析】试题分析：（1）连接OD，因为DE为⊙O的切线，所以OD⊥DE，又OC⊥OB，然后根据互余的关系可证∠1=∠2；（2）由（1）中∠1=∠2可得EF=ED，设DE=x，在Rt△ODE中，由勾股定理求得x =4，然后证Rt△EOD∽Rt△EGA．可求出AG的长．

试题解析：（1）证明：如图，连接OD，

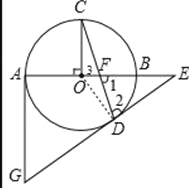
∵DE为⊙O的切线，∴OD⊥DE．∴∠ODE=90°，即∠2 ∠ODC=90°，∵OC=OD，∴∠C=∠ODC．∴∠2 ∠C=90°．∵OC⊥OB，∴∠C ∠3=90°．∴∠2=∠3,∵∠1=∠3，∴∠1=∠2．

（2）∵OF：OB=1：3，⊙O的半径为3，∴OF=1．∵∠1=∠2，∴EF=ED，在Rt△ODE中，OD=3，设DE=x，则EF=x，OE=1+x，所以，解得x =4．∴DE=4，OE=5．

∵AG为⊙O的切线，∴AG⊥AE．∴∠GAE=90°．∴∠ODE=∠GAE，∵∠OED=∠GEA，∴Rt△EOD∽Rt△EGA． 解得AG=6．

关闭