【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
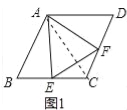
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
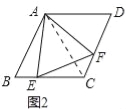
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
参考答案:
【答案】(1)AE=EF=AF;(2)证明过程见解析;(3)3-![]()
【解析】
试题分析:(1)结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形;(2)欲证明BE=CF,只要证明△BAE≌△CAF即可;(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题.
试题解析:(1)结论AE=EF=AF.
理由:如图1中,连接AC, ∵四边形ABCD是菱形,∠B=60°, ∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形, ∴∠BAC=∠DAC=60° ∵BE=EC, ∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°, ∴∠CAF=∠DAF=30°, ∴AF⊥CD, ∴AE=AF(菱形的高相等),
∴△AEF是等边三角形, ∴AE=EF=AF.
(2)如图2中,∵∠BAC=∠EAF=60°, ∴∠BAE=∠CAE,
在△BAE和△CAF中,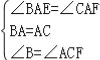 , ∴△BAE≌△CAF, ∴BE=CF.
, ∴△BAE≌△CAF, ∴BE=CF.
(3)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H, ∵∠EAB=15°,∠ABC=60°, ∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4, ∴BG=2,AG=2![]() ,在RT△AEG中,∵∠AEG=∠EAG=45°,
,在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() , ∴EB=EG﹣BG=2
, ∴EB=EG﹣BG=2![]() ﹣2, ∵△AEB≌△AFC,
﹣2, ∵△AEB≌△AFC,
∴AE=AF,EB=CF=2![]() ﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
∴∠AEF=∠AFE=60° ∵∠AEB=45°,∠AEF=60°, ∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°, ∴∠EFH=75°, ∵∠AFE=60°, ∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°, 在RT△CHF中,∵∠CFH=30°,CF=2![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2![]() ﹣2)
﹣2)![]() =3﹣
=3﹣![]() . ∴点F到BC的距离为3﹣
. ∴点F到BC的距离为3﹣![]() .
.
-
科目: 来源: 题型:
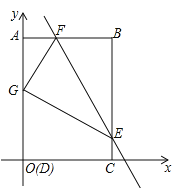
查看答案和解析>>【题目】如图,四边形ABCD为矩形,C点在
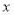 轴上,A点在
轴上,A点在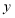 轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).(1)求G点坐标
(2)求直线EF解析式
(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )

A. 183 B. 157 C. 133 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=x2+3xy+x-
 ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位需以“挂号信”或“特快专递”方式向五所学校各寄一封信,这五封信的重量分别是
 .根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:
.根据这五所学校的地址及信件的重量范围,在邮局查得相关邮费标准如下:业务种类
计费单位
资费标准/元
挂号费/(元/封)
特制信封(元/个)
挂号信
首重100g,每重20g
0.8
3
0.5
续重101~2000g,每重100g
2.00
特制信封
首重1000g内
5.00
3
1.0
(1)重量为90g的信若以“挂号信”方式寄出,邮寄费为多少元?若以“特快专递”方式寄出呢?
(2)这五封信分别以怎样的方式寄出最合算?请说明理由.
(3)通过解答上述问题,你有何启示?(请你用一两句话说明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.

相关试题

