【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于![]() 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
参考答案:
【答案】(1)![]()
(2)存在点![]() ,使△ACP的面积最大
,使△ACP的面积最大
(3)存在点Q,坐标为:![]() ,
,![]()
【解析】
试题分析:26.解:(1)由抛物线![]() 过点A(-3,0),B(1,0),
过点A(-3,0),B(1,0),
则![]() …………………………………………………………1分
…………………………………………………………1分
解得 ………………………………………………………………2分
………………………………………………………………2分
∴二次函数的关系解析式![]() .…………………………3分
.…………………………3分
(2)连接PO,作PM⊥x轴于M,PN⊥y轴于N.…4分

设点P坐标为(m,n),则![]() .
.
PM =![]() ,
,![]() ,AO=3.(5分)
,AO=3.(5分)
当![]() 时,
时,![]() =2.
=2.
∴OC=2.……………………………………………………………6分
![]() =
=![]()
=![]() =
=![]() .8分
.8分
∵![]() =-1<0,∴当
=-1<0,∴当![]() 时,函数
时,函数![]()
![]() 有最大值.
有最大值.
此时![]()
![]() =
=![]() . …………9分
. …………9分
∴存在点![]() ,使△ACP的面积最大. ……………………………10分
,使△ACP的面积最大. ……………………………10分
(3)存在点Q,坐标为:![]() ,
,![]() . ………………………12分
. ………………………12分
分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明每天早上要在7:50之前赶到距家900米的学校上学.小明以60米/分的速度出发10分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以160米/分的速度去追小明,爸爸能否在小明进学校前追上他?若能,请说明理由,若不能,请计算,爸爸的速度至少为多少时才能赶在小明进学校前追上他?
-
科目: 来源: 题型:
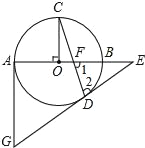
查看答案和解析>>【题目】如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形
(1)
(2)
(3)
……
黑色瓷砖的块数
4
……
黑白两种瓷砖的总块数
15
……
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=
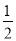 AB时,求t的值.
AB时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

相关试题

