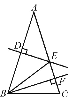
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
参考答案:
【答案】36°
【解析】
试题设∠A==x,根据线段垂直平分线的性质可得∠A=∠ABE=x,∠BEC=∠C,由三角形的外角的性质可得∠BEC=∠A+∠ABE=2x,又因△ABC是等腰三角形可得∠ABC=∠C=2x,在△ABC中,根据三角形的内角和定理列方程即可求得x.
试题解析:解:连接BE,
∵DE是线段AB的垂直平分线,
∴AE=BE
∴∠A=∠ABE,
设∠A=∠ABE=x,
∴∠BEC=∠A+∠ABE=2x,
∵CE的垂直平分线正好经过点B,与AC相交于点可知△BCE是等腰三角形,
∴∠BEC=∠C=2x,
∵△ABC是等腰三角形,
∴∠ABC=∠C=2x,
在△ABC中,∠ABC+∠C+∠A=180°,即2x+2x+x=180°,解得x=36°,
∴∠A=36°.
-
科目: 来源: 题型:
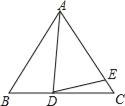
查看答案和解析>>【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),抛物线y=x2﹣2x+k与x轴交于A,B两点,与y轴交于点C(0,﹣3).
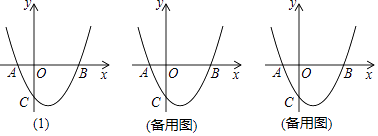
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求出点Q坐标,使△BCQ是以BC为直角边的直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
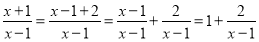 ,
, ,则
,则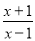 和
和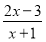 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,不属于“和谐分式”的是 (填序号).
①
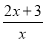 ②
②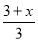 ③
③ ④
④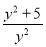
(2)将“和谐分式”
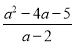 化成一个整式与一个分子为常数的分式的和的形式.
化成一个整式与一个分子为常数的分式的和的形式.(3)应用:先化简
 ,并求
,并求 取什么整数时,该式的值为整数.
取什么整数时,该式的值为整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=  BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
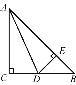
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.
(1)若CD=6
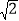 ,求AC的长;
,求AC的长;(2)求证:AB-AC=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
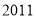 、
、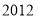 ……
……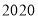 这
这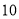 个数中,不能表示成两个平方数差的数有________个.
个数中,不能表示成两个平方数差的数有________个.
相关试题

