【题目】如图(1),抛物线y=x2﹣2x+k与x轴交于A,B两点,与y轴交于点C(0,﹣3).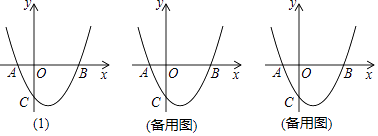
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求出点Q坐标,使△BCQ是以BC为直角边的直角三角形.
参考答案:
【答案】
(1)﹣3,(﹣1,0),(3,0)
(2)解:y=x2﹣2x﹣3=(x﹣1)2﹣4,则M(1,﹣4),
抛物线的对称轴交x轴于N,如图(1), 
四边形ABMC的面积=S△AOC+S梯形OCMN+S△MNB= ![]() ×1×3+
×1×3+ ![]() ×(3+4)×1+
×(3+4)×1+ ![]() ×4×(3﹣1)=9
×4×(3﹣1)=9
(3)解:存在.
作DE∥y轴交直线BC于E,如图(2), 
设直线BC的解析式为y=kx+b,
把B(3,0),C(0,﹣3)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x﹣3,
设D(x,x2﹣2x﹣3),则E(x,x﹣3),
∴DE=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△BCD= ![]() DE3=﹣
DE3=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
当x= ![]() 时,S△BCD有最大值,
时,S△BCD有最大值,
∵S△ACB= ![]() ×4×3=6,
×4×3=6,
∴x= ![]() 时,四边形ABDC的面积最大,
时,四边形ABDC的面积最大,
此时D点坐标为( ![]() ,﹣
,﹣ ![]() );
);
(4)解:∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴∠OCB=∠OBC=45°,
当∠CBQ=90°时,BQ交y轴于G点,如图(3),则∠OBG=45°,
∴OG=OB=3,则G(0,3),
易得直线BG的解析式为y=﹣x+3,
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,
,
∴Q(﹣2,5);
当∠BCQ=90°时,CQ交x轴于H点,如图(3), 
则∠OCH=45°,
∴OH=OC=3,则H(﹣3,0),
易得直线CH的解析式为y=﹣x﹣3,
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,
,
∴Q(1,﹣2);
综上所述,点Q坐标为(1,﹣2)或(2,5)时,使△BCQ是以BC为直角边的直角三角形.
【解析】解:(1)把C(0,﹣3)代入y=x2﹣2x+k得k=﹣3,
则抛物线解析式为y=x2﹣2x﹣3,
当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0);
所以答案是﹣3,(﹣1,0),(3,0);
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期
卖出甲商品的数量(个)
卖出乙商品的数量(个)
收入(元)
第一天
39
21
321
第二天
26
14
204
第三天
39
25
345
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=
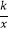 (x>0)的图象与边BC交与点F.
(x>0)的图象与边BC交与点F.
(1)若△OAE、△OCF的面积分别为S1、S2 , 且S1+S2=2,求k的值;
(2)在(1)的结论下,当OA=2,OC=4时,求三角形OEF的面积. -
科目: 来源: 题型:
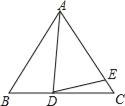
查看答案和解析>>【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
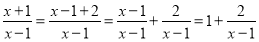 ,
, ,则
,则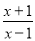 和
和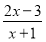 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,不属于“和谐分式”的是 (填序号).
①
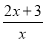 ②
②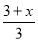 ③
③ ④
④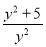
(2)将“和谐分式”
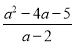 化成一个整式与一个分子为常数的分式的和的形式.
化成一个整式与一个分子为常数的分式的和的形式.(3)应用:先化简
 ,并求
,并求 取什么整数时,该式的值为整数.
取什么整数时,该式的值为整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
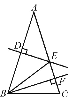
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=  BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
相关试题

