【题目】在![]() 、
、![]() ……
……![]() 这
这![]() 个数中,不能表示成两个平方数差的数有________个.
个数中,不能表示成两个平方数差的数有________个.
参考答案:
【答案】2
【解析】
首先将符合条件的整数分解成两整数的和与这两整数的差的积,再由整数的奇偶性,判断这个符合条件的整数,是奇数或是能被4整除的数,从而找出符合条件的整数的个数.在2011、2012、…、2020这10个数中,奇数有5个,能被4整除的有3个,所以不能表示成两个平方数差的数有10-5-3=2个.
对x=n2m2=(n+m)(nm),(m<n,m,n为整数)
因为n+m与nm同奇同偶,所以x是奇数或是4的倍数,
在2011、2012、…、2020这10个数中,奇数有5个,能被4整除的数有3个,
所以能表示成两个平方数差的数有5+3=8个,
则不能表示成两个平方数差的数有108=2个.
故答案为:2
-
科目: 来源: 题型:
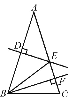
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=  BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
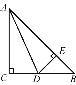
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.
(1)若CD=6
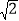 ,求AC的长;
,求AC的长;(2)求证:AB-AC=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划用
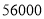 元从厂家进
元从厂家进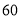 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型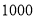 元/台,每台获利
元/台,每台获利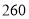 元;乙型
元;乙型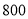 元/台,每台获利
元/台,每台获利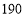 元;丙型
元;丙型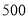 元/台,每台获利
元/台,每台获利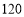 元.设甲、乙型设备应各买入
元.设甲、乙型设备应各买入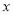 ,
,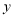 台:
台:(1)购买丙型设备 台(用含
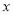 ,
,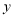 的代数式表示);
的代数式表示);(2)若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
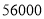 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?(3)在第(2)题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
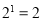 ,
,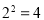 ,
,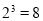 ,
,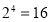 ,
,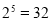 ,
,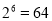 ,
,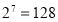 ,
,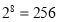 ,……
,……(1)请你据此推测出
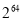 的个位数字是几?
的个位数字是几?(2)利用上面的结论,求
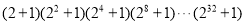 的个位数字.
的个位数字.(3)
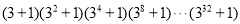 的个位数字又是多少?
的个位数字又是多少? -
科目: 来源: 题型:
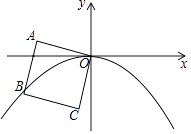
查看答案和解析>>【题目】如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
A.
B.
C.﹣2
D.
相关试题

