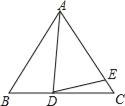
【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
参考答案:
【答案】(1)5(2)20,10(3)α=2β,理由见解析.
【解析】
(1)先求出∠BAC=40°,再利用等腰三角形的性质求出∠B,∠ADE,根据三角形外角的性质求出∠ADC,减去∠ADE,即可得出结论;
(2)先利用等腰三角形的性质求出∠DAE,进而求出∠BAD,即可得出结论;
(3)利用等腰三角形的性质和三角形外角和定理即可得出结论.
(1)∵∠BAD=10°,∠DAE=30°,
∴∠BAC=∠BAD+∠DAE=40°,
∵AB=AC,
∴∠B=∠C=![]() (180°﹣∠BAC)=70°.
(180°﹣∠BAC)=70°.
∵AD=AE,∠DAE=30°,
∴∠ADE=∠AED=![]() (180°﹣∠DAE)=75°.
(180°﹣∠DAE)=75°.
∵∠B=70°,∠BAD=10°,
∴∠ADC=∠B+∠BAD=80°,
∴∠EDC=∠ADC﹣∠ADE=5°.
故答案为5;
(2)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°﹣2∠ADE=40°,
∴∠BAD=60°﹣40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴∠CDE=∠ADC﹣∠ADE=10°,
故答案为:20,10;
(3)猜想:α=2β.理由如下:
设∠B=x,∠AED=y,
∵AB=AC,AD=AE,
∴∠C=∠B=x,∠ADE=∠AED=y.
∵∠AED=∠CDE+∠C,
∴y=β+x,
∵∠ADC=∠BAD+∠B=∠ADE+∠CDE,
∴α+x=y+β=β+x+β,
∴α=2β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.

(1)他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图②).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)如果要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片 张,3号卡片 张;
(3)当他拼成如图③所示的长方形,根据6张小纸片的面积和等于打纸片(长方形)的面积可以把多项式a2+3ab+2b2分解因式,其结果是 ;
(4)动手操作,请你依照小刚的方法,利用拼图分解因式a2+5ab+6b2= 画出拼图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期
卖出甲商品的数量(个)
卖出乙商品的数量(个)
收入(元)
第一天
39
21
321
第二天
26
14
204
第三天
39
25
345
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=
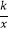 (x>0)的图象与边BC交与点F.
(x>0)的图象与边BC交与点F.
(1)若△OAE、△OCF的面积分别为S1、S2 , 且S1+S2=2,求k的值;
(2)在(1)的结论下,当OA=2,OC=4时,求三角形OEF的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),抛物线y=x2﹣2x+k与x轴交于A,B两点,与y轴交于点C(0,﹣3).
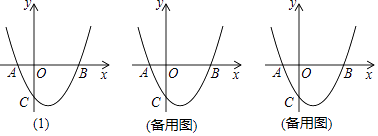
(1)k= , 点A的坐标为 , 点B的坐标为;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由;
(4)在抛物线y=x2﹣2x+k上求出点Q坐标,使△BCQ是以BC为直角边的直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
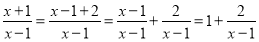 ,
, ,则
,则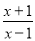 和
和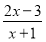 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,不属于“和谐分式”的是 (填序号).
①
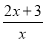 ②
②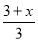 ③
③ ④
④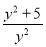
(2)将“和谐分式”
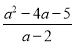 化成一个整式与一个分子为常数的分式的和的形式.
化成一个整式与一个分子为常数的分式的和的形式.(3)应用:先化简
 ,并求
,并求 取什么整数时,该式的值为整数.
取什么整数时,该式的值为整数. -
科目: 来源: 题型:
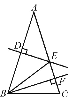
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
相关试题

