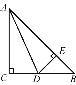
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.
(1)若CD=6![]() ,求AC的长;
,求AC的长;
(2)求证:AB-AC=CD.
参考答案:
【答案】(1)AC=BC=12+6![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由∠C=90°,AD是∠BAC的角平分线,DE⊥AB,根据角平分线的性质,即可得CD=DE,又由在△ABC中,AC=BC,∠C=90°,根据等腰三角形的性质,可求得AC=BC,∠B=45°,然后利用勾股定理,即可求得AC的长;
(2)首先证得AC=AE,又由(1)易得CD=DE=BE,然后利用线段的和差关系与等量代换的知识,即可求得AB-AC=CD.
(1)∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=6![]() ,
,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
在Rt△BDE中,由勾股定理得:BD=12
∴AC=BC=CD+BD=12+6![]() ;
;
(2)∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD,
∵∠C=90°,
∴AC⊥BC,
∵DE⊥AB,
∴∠ADC=∠ADE,
又∵AD=AD,
∴△ADC≌△ADE,
∴AE=AC,
∵CD=DE,DE=BE,
∴CD=BE,
∴AB-AC=AB-AE=BE=CD,
即:AB-AC=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
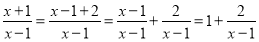 ,
, ,则
,则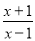 和
和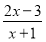 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,不属于“和谐分式”的是 (填序号).
①
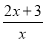 ②
②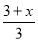 ③
③ ④
④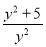
(2)将“和谐分式”
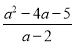 化成一个整式与一个分子为常数的分式的和的形式.
化成一个整式与一个分子为常数的分式的和的形式.(3)应用:先化简
 ,并求
,并求 取什么整数时,该式的值为整数.
取什么整数时,该式的值为整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,连接BE,求∠A的度数.
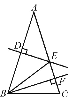
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=  BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
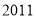 、
、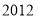 ……
……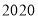 这
这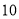 个数中,不能表示成两个平方数差的数有________个.
个数中,不能表示成两个平方数差的数有________个. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划用
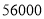 元从厂家进
元从厂家进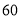 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,其中甲型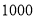 元/台,每台获利
元/台,每台获利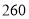 元;乙型
元;乙型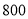 元/台,每台获利
元/台,每台获利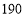 元;丙型
元;丙型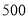 元/台,每台获利
元/台,每台获利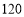 元.设甲、乙型设备应各买入
元.设甲、乙型设备应各买入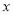 ,
,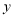 台:
台:(1)购买丙型设备 台(用含
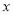 ,
,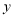 的代数式表示);
的代数式表示);(2)若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
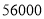 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?(3)在第(2)题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
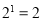 ,
,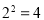 ,
,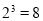 ,
,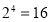 ,
,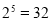 ,
,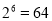 ,
,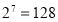 ,
,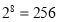 ,……
,……(1)请你据此推测出
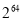 的个位数字是几?
的个位数字是几?(2)利用上面的结论,求
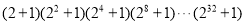 的个位数字.
的个位数字.(3)
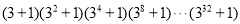 的个位数字又是多少?
的个位数字又是多少?
相关试题

