【题目】如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠F= . 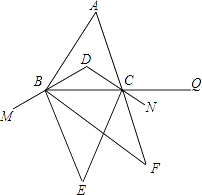
参考答案:
【答案】15°
【解析】解:∵BD、CD分别平分∠ABC、∠ACB,∠A=60°,
∴∠DBC= ![]() ∠ABC,∠DCB=
∠ABC,∠DCB= ![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=
(180°﹣∠A)= ![]() ×(180°﹣60°)=60°,
×(180°﹣60°)=60°,
∴∠MBC+∠NCB=360°﹣60°=300°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠5+∠6= ![]() ∠MBC,∠1=
∠MBC,∠1= ![]() ∠NCB,
∠NCB,
∴∠5+∠6+∠1= ![]() (∠NCB+∠NCB)=150°,
(∠NCB+∠NCB)=150°,
∴∠E=180°﹣(∠5+∠6+∠1)=180°﹣150°=30°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,
即∠2=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E,
∴∠F= ![]() ∠E=
∠E= ![]() ×30°=15°.
×30°=15°.
故答案为15°.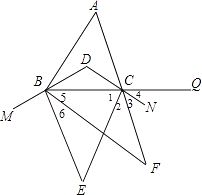
先由BD、CD分别平分∠ABC、∠ACB得到∠DBC= ![]() ∠ABC,∠DCB=
∠ABC,∠DCB= ![]() ∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB=
∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=
(180°﹣∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6= ![]() ∠MBC,∠1=
∠MBC,∠1= ![]() ∠NCB,两式相加得到∠5+∠6+∠1=
∠NCB,两式相加得到∠5+∠6+∠1= ![]() (∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F=
(∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F= ![]() ∠E.
∠E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(b+3a)+2(3﹣5a)﹣(6﹣2b),其中:a=﹣1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式5x-12≤2(4x-3),并求出负整数解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长是方程x2﹣5x+6=0的两个根,则三角形的第三边c的取值范围是 .
-
科目: 来源: 题型:
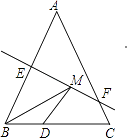
查看答案和解析>>【题目】如图,等腰△ABC底边BC的长为4cm,面积是12cm2 , 腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“劳动周”的到来,某校将九(1)班50名学生本周的课后劳动时间比上周都延长了10分钟,则该班学生本周劳动时间的下列数据与上周比较不发生变化的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
相关试题

