【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

参考答案:
【答案】PA=PB;成立;PA=PB.
【解析】试题分析:(1)根据三角形CBD是直角三角形,而且点P为线段CD的中点,应用直角三角形的性质,可得PA=PB,据此解答即可.(2)首先过C作CE⊥n于点E,连接PE,然后分别判断出PC=PE、∠PCA=∠PEB、AC=BE;然后根据全等三角形判定的方法,判断出△PAC∽△PBE,即可判断出PA=PB仍然成立.(3)首先延长AP交直线n于点F,作AE⊥BD于点E,然后根据相似三角形判定的方法,判断出△AEF∽△BPF,即可判断出AFBP=AEBF,再个AF=2PA,AE=2k,BF=AB,可得2PAPB=2k.AB,所以PAPB=kAB,据此解答即可
试题解析:(1)∵l⊥n, ∴BC⊥BD, ∴三角形CBD是直角三角形, 又∵点P为线段CD的中点,
∴PA=PB.
把直线l向上平移到如图②的位置,PA=PB仍然成立,理由如下:
如图②,过C作CE⊥n于点E,连接PE,
 ,
,
∵三角形CED是直角三角形,点P为线段CD的中点, ∴PD=PE, 又∵点P为线段CD的中点,
∴PC=PD, ∴PC=PE; ∵PD=PE, ∴∠CDE=∠PEB, ∵直线m∥n, ∴∠CDE=∠PCA,
∴∠PCA=∠PEB, 又∵直线l⊥m,l⊥n,CE⊥m,CE⊥n, ∴l∥CE, ∴AC=BE,
在△PAC和△PBE中, ∴△PAC∽△PBE, ∴PA=PB.
∴△PAC∽△PBE, ∴PA=PB.
(3)如图③,延长AP交直线n于点F,作AE⊥BD于点E,
 ,
,
∵直线m∥n, ∴![]() , ∴AP=PF, ∵∠APB=90°, ∴BP⊥AF, 又∵AP=PF, ∴BF=AB;
, ∴AP=PF, ∵∠APB=90°, ∴BP⊥AF, 又∵AP=PF, ∴BF=AB;
在△AEF和△BPF中,![]() ∴△AEF∽△BPF, ∴
∴△AEF∽△BPF, ∴![]() , ∴AFBP=AEBF,
, ∴AFBP=AEBF,
∵AF=2PA,AE=2k,BF=AB, ∴2PAPB=2k.AB, ∴PAPB=kAB. ∴PA=PB
-
科目: 来源: 题型:
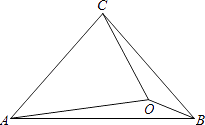
查看答案和解析>>【题目】△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
A.55°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(b+3a)+2(3﹣5a)﹣(6﹣2b),其中:a=﹣1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式5x-12≤2(4x-3),并求出负整数解.
-
科目: 来源: 题型:
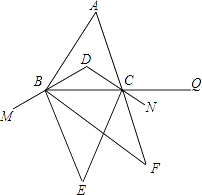
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠F= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形两边长是方程x2﹣5x+6=0的两个根,则三角形的第三边c的取值范围是 .
-
科目: 来源: 题型:
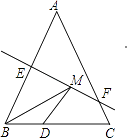
查看答案和解析>>【题目】如图,等腰△ABC底边BC的长为4cm,面积是12cm2 , 腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为cm.
相关试题

