【题目】如图,已知![]() ,
,![]() .说明
.说明![]() 的理由.
的理由.
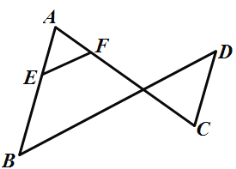
解:∵![]() (已知),
(已知),
∴________//________(_______________)
∴![]() (_______________)
(_______________)
∵![]() (________),
(________),
∴![]() (_______________)
(_______________)
∵![]() (己证),
(己证),
∴![]() (_______________).
(_______________).
参考答案:
【答案】AB,CD,内错角相等,两直线平行,两直线平行,内错角相等,已知,两直线平行,同位角相等,等量代换.
【解析】
根据∠A=∠C可得到AB∥CD,再根据两直线平行,内错角相等可得∠B=∠D,首先根据EF∥BD可得到∠AEF=∠B,再由(1)中证出的∠B=∠D可利用等量代换得到∠AEF=∠D.
解:∵∠A=∠C,(已知)
∴AB∥CD,(内错角相等,两直线平行)
∴∠D=∠B,(两直线平行,内错角相等)
∵EF∥DB,(已知)
∴∠AEF=∠B(两直线平行,同位角相等)
∵∠D=∠B(已证)
∴∠AEF=∠D(等量代换)
故答案为:AB,CD,内错角相等,两直线平行,两直线平行,内错角相等,已知,两直线平行,同位角相等,等量代换.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写推理的依据。
(1)已知:AB∥CD,AD∥BC。求证:∠B=∠D。
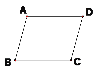
证明:∵AB∥CD,AD∥BC( 已知 )
∴∠A+∠B=180,∠A+∠D=180°(_______________________________)
∴∠B=∠D (___________________________)
(2)已知:DF∥AC,∠A=∠F。求证:AE∥BF。
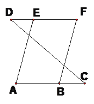
证明:∵DF∥AC (已知)
∴∠FBC=∠_______(_______________________________)
∵∠A=∠F(已知)
∴∠A=∠FBC (____________________)
∴AE∥FB (_____________________________)
-
科目: 来源: 题型:
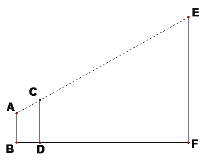
查看答案和解析>>【题目】(1)在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面。若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度。
(2)如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6),点C是线段AB的中点。请问在x轴上是否存在一点P,使得以P、A、C为顶点的三角形与△AOB相似?若存在,求出P点坐标(写出计算的过程);若不存在,说明理由。
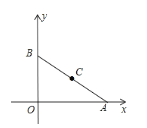
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋内装有四张完全相同的卡片,分别标有数字1、2、3、4。
(1)若任取一张卡片,上面所标数字是不小于3的概率为;
(2)在口袋中任取两张卡片:请你利用树状图或列表法求出这两张卡片上的数字的积为奇数的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD、ADEF都是菱形,∠BAD=∠FAD, ∠BAD为锐角.
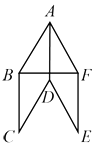
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数。
相关试题

