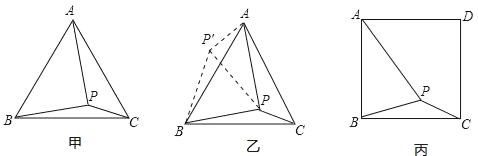
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
参考答案:
【答案】(1)等边 直角 150°;(2)![]() ;(3)135°;(4)
;(3)135°;(4)![]() .
.
【解析】
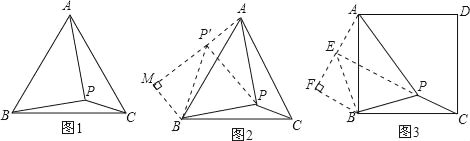
(1)将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,
(2)过点B作BM⊥AP′,交AP′的延长线于点M,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
(3)求出![]() ,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
解:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP′,
∴![]()
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴![]()
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,则△PP′A是 直角三角形;
∴∠BPC=∠AP′B=90°+60°=150°;
(2)过点B作BM⊥AP′,交AP′的延长线于点M,
∴![]()
由勾股定理得: ![]()
∴![]()
由勾股定理得: ![]()
故答案为:(1)等边;直角;150;![]() ;
;
(3)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴![]() ,
,
由勾股定理得:EP=2,
∵![]()
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:(3)∠BPC的度数是135°;
(4)正方形ABCD的边长是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果
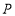 处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
A.10010B.10101
C.10100D.10110
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某勘测队在一条近似笔直的河流l两边勘测(河宽忽略不计),共设置了A,B,C三个勘测点.
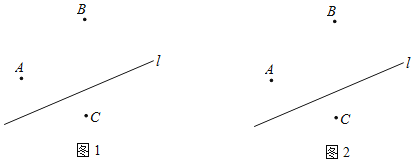
(1)若勘测队在A点建一水池,现将河水引入到水池A中,则在河岸的什么位置开沟,才能使水沟的长度最短?请在图1中画出图形;你画图的依据是 .
(2)若勘测队在河岸某处开沟,使得该处到勘测点B,C所挖水沟的长度之和最短,请在图2中画出图形;你画图的依据是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)和点B,化简
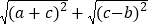 的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )
的结果为: ①c;②;③b﹣a;④a﹣b+2c.其中正确的有( )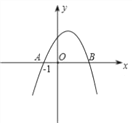
A. 一个 B. 两个 C. 三个 D. 四个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中小明离家的距离y(km)与时间x(min)之间的对应关系.根据图象,下列说法中正确的是( )
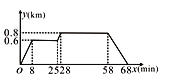
A. 小明吃早餐用了17min
B. 食堂到图书馆的距离为0.8km
C. 小明读报用了28min
D. 小明从图书馆回家的速度为0.8km/min
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭
 出发,晚上停留在
出发,晚上停留在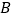 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,-8,+10,-12,+6,-18,+5,-2.
(1)
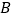 处在岗亭
处在岗亭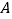 的什么方向?距离岗亭
的什么方向?距离岗亭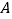 多远?
多远?(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于点M,N,给出下列结论:①△ABM≌△CDN;②AM=
 AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB= S△ABC,其中正确的结论是__ __.(填序号)
S△ABC,其中正确的结论是__ __.(填序号)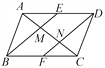
相关试题

