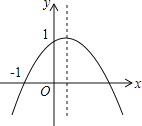
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
参考答案:
【答案】①③④
【解析】由抛物线的对称轴在y轴右侧,可以判定a、b异号,由此确定①正确;由抛物线与x轴有两个交点得到b2-4ac>0,又抛物线过点(0,1),得出c=1,由此判定②错误;由抛物线过点(-1,0),得出a-b+c=0,即a=b-1,由a<0得出b<1;由a<0,及ab<0,得出b>0,由此判定④正确;由a-b+c=0,及b>0得出a+b+c=2b>0;由b<1,c=1,a<0,得出a+b+c<a+1+1<2,由此判定③正确;由图象可知,当自变量x的取值范围在一元二次方程ax2+bx+c=0的两个根之间时,函数值y>0,由此判定⑤错误.
∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(-1,0), ∴c=1,a-b+c=0.
①∵抛物线的对称轴在y轴右侧,∴x=-![]() >0, ∴a与b异号,∴ab<0,正确;
>0, ∴a与b异号,∴ab<0,正确;
②∵抛物线与x轴有两个不同的交点,∴b2-4ac>0, ∵c=1,∴b2-4a>0,b2>4a,错误;
④∵抛物线开口向下,∴a<0,∵ab<0,∴b>0.∵a-b+c=0,c=1,∴a=b-1,
∵a<0,∴b-1<0,b<1,∴0<b<1,正确;
③∵a-b+c=0,∴a+c=b,∴a+b+c=2b>0.∵b<1,c=1,a<0,
∴a+b+c=a+b+1<a+1+1=a+2<0+2=2, ∴0<a+b+c<2,正确;
⑤抛物线y=ax2+bx+c与x轴的一个交点为(-1,0),设另一个交点为(x0,0),则x0>0,
由图可知,当x0>x>-1时,y>0,错误; 综上所述,正确的结论有①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知平行四边形ABCD,BC∥x轴,BC=6,点A的坐标为(1,4),点B的坐标为(﹣3,﹣4),点C在第四象限,点P是平行四边形ABCD边上的一个动点.
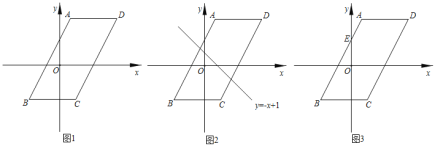
(1)若点P在边CD上,BC=CP,求点P的坐标;
(2)如图2,若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=﹣x+1上,求点P的坐标;
(3)若点P在边AB,AD,BC上,点E是AB与y轴的交点,如图3,过点P作y轴的平行线PF,过点E作x轴的平行线E,它们相交于点F,将△PEF沿直线PE翻折,当点F的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=
 ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .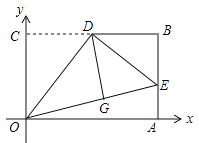
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人准备玩传球游戏.规则是:第1次传球从甲开始,甲先将球随机传给乙、丙两人中的一个人,再由接到球的人随机传给其他两人中的一个人…如此反复.
(1)若传球1次,球在乙手中的概率为 ;
(2)若传球3次,求球在甲手中的概率(用树状图或列表法求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m﹣1)x+m2=0有实数根.
(1)求m的取值范围;
(2)若两根为x1、x2且x12+x22=7,求m的值.
相关试题

