【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

参考答案:
【答案】(1)26°;(2)8.
【解析】试题分析:(1)根据垂径定理,得到![]() ,再根据圆周角与圆心角的关系,得知∠E=
,再根据圆周角与圆心角的关系,得知∠E=![]() ∠O,据此即可求出∠DEB的度数;
∠O,据此即可求出∠DEB的度数;
(2)由垂径定理可知,AB=2AC,在Rt△AOC中,OC=3,OA=5,由勾股定理求AC即可得到AB的长.
试题解析:(1)∵AB是⊙O的一条弦,OD⊥AB,
∴![]() ,
,
∴∠DEB=![]() ∠AOD=
∠AOD=![]() ×52°=26°;
×52°=26°;
(2)∵AB是⊙O的一条弦,OD⊥AB,
∴AC=BC,即AB=2AC,
在Rt△AOC中,AC=![]() =
=![]() =4,
=4,
则AB=2AC=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=
 ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .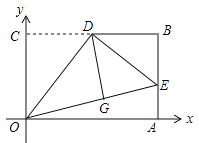
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
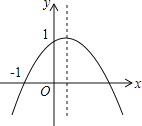
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人准备玩传球游戏.规则是:第1次传球从甲开始,甲先将球随机传给乙、丙两人中的一个人,再由接到球的人随机传给其他两人中的一个人…如此反复.
(1)若传球1次,球在乙手中的概率为 ;
(2)若传球3次,求球在甲手中的概率(用树状图或列表法求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m﹣1)x+m2=0有实数根.
(1)求m的取值范围;
(2)若两根为x1、x2且x12+x22=7,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点O是边BC的中点,连接AO并延长,交DC延长线于点E,连接AC,BE.
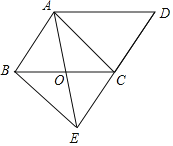
(1)求证:四边形ABEC是平行四边形;
(2)当∠D=50°,∠AOC=100°时,判断四边形ABEC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中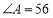 °,
°,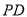 垂直平分
垂直平分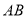 ,
,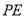 垂直平分
垂直平分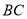 ,则
,则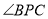 的度数为( )
的度数为( )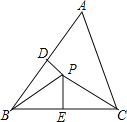
A.124°B.112°C.108°D.118°
相关试题

