【题目】如图1,已知平行四边形ABCD,BC∥x轴,BC=6,点A的坐标为(1,4),点B的坐标为(﹣3,﹣4),点C在第四象限,点P是平行四边形ABCD边上的一个动点.
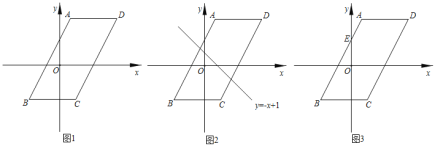
(1)若点P在边CD上,BC=CP,求点P的坐标;
(2)如图2,若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=﹣x+1上,求点P的坐标;
(3)若点P在边AB,AD,BC上,点E是AB与y轴的交点,如图3,过点P作y轴的平行线PF,过点E作x轴的平行线E,它们相交于点F,将△PEF沿直线PE翻折,当点F的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)
参考答案:
【答案】(1)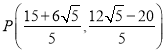 ;(2)P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);(3)(-
;(2)P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);(3)(-![]() ,﹣3)或(2,4)或(
,﹣3)或(2,4)或(![]() ,﹣4).
,﹣4).
【解析】
(1)根据平行四边形性质可求得点C、D坐标,再利用待定系数法求直线CD解析式,根据点P在边CD上,BC=CP,可设P(t,2t10),运用两点间距离公式或勾股定理可建立关于t的方程,解方程即可求得P的坐标;
(2)先运用待定系数法求直线AB解析式和直线AD解析式,根据点P关于坐标轴对称的点Q落在直线y=x+1上,分两种情况:①如图2,点P在边AB,AD上,点P关于x轴对称的点Q落在直线y=x+1上,②如图3,点P在边AB,AD上,点P关于y轴对称的点Q落在直线y=x+1上,分别求得点P的坐标即可;
(3)分三种情况:①若点P在边AB上,②若点P在边AD上,③若点P在边BC上,运用翻折性质、勾股定理分别求出点P的坐标.
解:(1)∵平行四边形ABCD
∴AD=BC=6,AB=CD,AB∥CD,AD∥BC
∵BC∥x轴,
∴AD∥x轴,
∵点A的坐标为(1,4),点B的坐标为(﹣3,﹣4),点C在第四象限,
∴C(3,﹣4),D(7,4)
设直线CD解析式为y=kx+b,则![]() ,解得
,解得![]() ,
,
∴直线CD解析式为y=2x﹣10,
∵点P在边CD上,BC=CP,设P(t,2t﹣10),
则(t﹣3)2+[2t﹣10﹣(﹣4)]2=36,
解得:t1=![]() (舍去),t2=
(舍去),t2=![]() ,
,
∴P(![]() ,
,![]() );
);
(2)∵A(1,4),B(﹣3,﹣4),D(7,4)
∴直线AB解析式为y=2x+2,直线AD解析式为y=4,
点P关于坐标轴对称的点Q落在直线y=﹣x+1上,分两种情况:
①如图2,点P在边AB,AD上,点P关于x轴对称的点Q落在直线y=﹣x+1上,
当点P在AB上时,设P(m,2m+2),则Q(m,﹣m+1)
∴2m+2+(﹣m+1)=0,
解得m=﹣3
∴P1(﹣3,﹣4),
当点P在AD上时,设P(m,4),则Q(m,﹣m+1)
∴4﹣m+1=0,
解得:m=5,
∴P2(5,4)
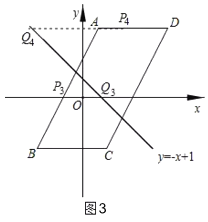
②如图3,点P在边AB,AD上,点P关于y轴对称的点Q落在直线y=﹣x+1上,
当点P在AB上时,设P(m,2m+2),则Q(﹣2m﹣1,2m+2)
∴m﹣2m﹣1=0,
解得:m=﹣1,
∴P3(﹣1,0)
当点P在AD上时,设P(m,4),则Q(﹣3,4),
∴m﹣3=0,
解得:m=3
∴P4(3,4),
综上所述,点P的坐标为:P1(﹣3,﹣4),P2(5,4),P3(﹣1,0),P4(3,4);
(3)在y=2x+2中,令x=0,则y=2,
∴E(0,2),
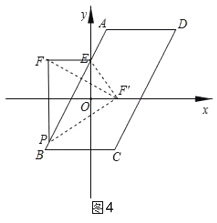
①若点P在边AB上,如图4设点P(m,2m+2),则F(m,2)
由翻折得:EF′=EF=﹣m,FF′⊥BE
设直线FF′解析式为y=k′x+b′,则k′=![]() ,
,
∴![]() m+b′=2,解得:b′=
m+b′=2,解得:b′=![]() m+2
m+2
∴直线FF′解析式为y=![]() x+
x+![]() m+2,
m+2,
令y=0,得x=m+4,
∴F′(m+4,0),
在Rt△OEF′中,OE2+OF′2=EF′2
∴22+(m+4)2=(﹣m)2,
解得:m=![]() ,
,
∴P(![]() ,﹣3),
,﹣3),
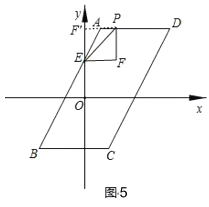
②若点P在边AD上,如图5设P(m,4),则F(m,2),
由题意可知,△PEF沿直线PE翻折后,点F的对应点F′落在y轴上,
由翻折得:EF′=EF=m,∠PEF=∠PEF′
∵EF⊥y轴
∴∠FEF′=90°
∴∠PEF=∠PEF′=45°
∴△PEF是等腰直角三角形
∴EF=PF,即m=2
∴P(2,4),
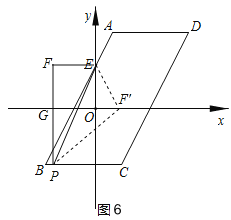
③若点P在边BC上,如图6设PF交x轴于点G,P(m,﹣4),则F(m,2)
∴PF=6,EF=﹣m,PG=4,
由翻折得:EF′=EF=﹣m,PF′=PF=6
∵PF⊥x轴
∴F′G=![]() ,
,
∴F′(m+![]() ,0)
,0)
在Rt△OEF′中,OE2+OF′2=EF′2
∴22+ ( m+![]() )2=m2,
)2=m2,
解得:m=![]() ,
,
∴P(![]() ,﹣4),
,﹣4),
综上所述,点P的坐标为(![]() ,﹣3)或(2,4)或(
,﹣3)或(2,4)或(![]() ,﹣4).
,﹣4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料.
在数学课上,老师请同学思考如下问题:
已知:如图①,在△ABC中,∠A=90°.

图①
求作:⊙P,使得点P在边AC上,且⊙P与AB,BC都相切.
小轩的主要作法如下:
如图②,

图②
(1)作∠ABC的平分线BF,与AC交于点P;
(2)以P为圆心,AP长为半径作⊙P,则⊙P即为所求.
老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是 ____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.

(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
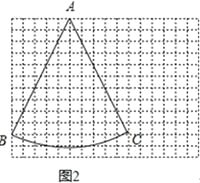
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若一直重型运输卡车P沿道路ON方向行驶的速度为18千米/时.

(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=
 ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .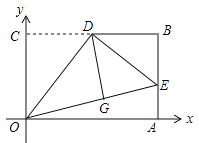
-
科目: 来源: 题型:
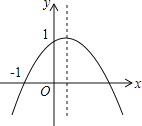
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.
相关试题

