【题目】在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( ) 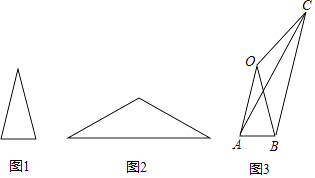
A.∠OCB=2∠ACB
B.∠OAB+∠OAC=90°
C.AC=2 ![]()
D.BC=4 ![]()
参考答案:
【答案】D
【解析】解:A、∵∠OBC=∠AOB, ∴OA∥BC,
∴∠OAC=∠ACB.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠ACB,
∴∠OCB=2∠ACB,结论A正确;
B、∵OA=OB,
∴∠OAB+∠AOB+∠OBA=180°.
∵∠OAC= ![]() ∠OCB=
∠OCB= ![]() ∠AOB,∠OAB=∠OBA,
∠AOB,∠OAB=∠OBA,
∴∠OAB+ ![]() ∠AOB=90°,即∠OAB+∠OAC=90°,结论B正确;
∠AOB=90°,即∠OAB+∠OAC=90°,结论B正确;
C、过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,如图4所示.
∵OA=OB,
∴∠AOE= ![]() ∠AOB=∠OAE.
∠AOB=∠OAE.
在△AOE和△OAE中, 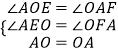 ,
,
∴△AOE≌△OAE(AAS),
∴AF=OE= ![]() =
= ![]() ,
,
∴AC=2AF=2 ![]() ,结论C正确;
,结论C正确;
D、过点B作BM⊥OA于点M,过点O作ON⊥BC于点N,如图5所示.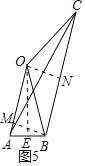
∵∠OAB+∠AOE=90°,∠MAB+∠ABM=90°,
∴∠AOE=∠ABM.
∵∠AEO=∠AMB=90°,
∴△AOE∽△ABM,
∴ ![]() ,
,
∴AM= ![]() ,OM=AO﹣AM=
,OM=AO﹣AM= ![]() .
.
∵BC∥AO,BM⊥AO,ON⊥BC,
∴四边形MBNO为矩形,
∴BN=OM= ![]() .
.
∵OB=OC,ON⊥BC,
∴BC=2BN=7,结论D错误.
故选D.
【考点精析】利用等腰三角形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(
 ,0)、B(3
,0)、B(3  ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A.2 ﹣2
﹣2
B.2
C.2
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是 .
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
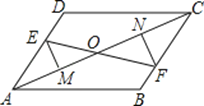
求证:(1)EM=FN;
(2)EF与MN互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个仓库共存有粮食60
 .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:(1)甲仓库运进粮食14
 ,乙仓库运出粮食10
,乙仓库运出粮食10 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?(2)如果甲仓库原有的粮食比乙仓库的2倍少3
 ,则甲仓库运出多少
,则甲仓库运出多少 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等? (3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1
 ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣
 x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 . 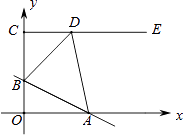
相关试题

