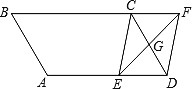
【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为![]()
(1)求证:无论![]() 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;
(2)①当![]() s时,CE⊥AD;
s时,CE⊥AD;
②当![]() 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.
参考答案:
【答案】(1)见解析;(2)①3.5;②2.
【解析】
(1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可;
(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,即可得出答案;
②求出△CDE是等边三角形,推出CE=DE,即可得出答案.
(1)四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
又∠CGF=∠EGD.
G是CD的中点,
CG=DG,
在△FCG和△EDG中,
∵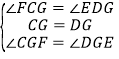 ,
,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)①当t=3.5s时,CE⊥AD,
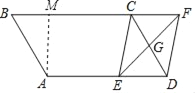
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
∵ ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
即CE⊥AD,
故答案为:3.5;
②当t=2s时,平行四边形CEDF的两条邻边相等,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
即平行四边形CEDF的两条邻边相等,
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,小明从中随机地抽取一张,把卡片上的数字做为被减数,将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,小华从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小明与小华做游戏,规则是:若这两数的差为非负数,则小明赢;否则,小华赢.你认为该游戏公平吗?请说明理由.如果不公平,请你修改游戏规则,使游戏公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区对参加2019年中考的300名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图.

请根据图表信息回答下列问题:
(1)
 __________,
__________, __________;
__________; (2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,据以上信息估计全区初中毕业生中视力正常的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=
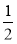 ,求AC的长.
,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
30
45
租金(元/辆)
450
600
已知某中学计划租用
 两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.(1)求最多能租用多少辆B型号客车?
(2)若七年级师生共有380人,请写出所有可能的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知线段
 ,点
,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,如图1所示.
,如图1所示.
(1)平移线段

 到线段
到线段
 ,使点
,使点 的对应点为,点
的对应点为,点 的对应点为
的对应点为 ,若点
,若点 的坐标为
的坐标为 ,求点
,求点 的坐标;
的坐标; (2)平移线段

 到线段
到线段
 ,使点
,使点 在
在 轴的正半轴上,点
轴的正半轴上,点 在第二象限内(
在第二象限内( 与
与 对应,
对应,  与
与 对应),连接
对应),连接 如图2所示.若
如图2所示.若 表示△BCD的面积),求点
表示△BCD的面积),求点 、
、 的坐标;
的坐标; (3)在(2)的条件下,在
 轴上是否存在一点
轴上是否存在一点 ,使
,使 表示△PCD的面积)?若存在,求出点
表示△PCD的面积)?若存在,求出点 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角形的绿地,量得两直角边长分别为6m和8m,现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
相关试题

