【题目】某区对参加2019年中考的300名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图.

请根据图表信息回答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,据以上信息估计全区初中毕业生中视力正常的学生有多少人?
参考答案:
【答案】(1)![]() ;(2)见解析;(3)估计全区初中毕业生中视力正常的学生有900人.
;(2)见解析;(3)估计全区初中毕业生中视力正常的学生有900人.
【解析】
(1)求出总人数即可解决问题.
(2)根据第四组人数画出直方图即可.
(3)利用样本估计总体的思想解决问题即可.
解:(1)总人数=50÷0.25=200(人),
∴a=200×0.25=50(人),
b=![]() .
.
故答案为50,![]()
(2)如下图:
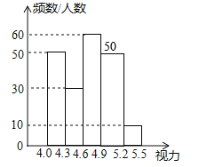
(3)![]() (人)
(人)
估计全区初中毕业生中视力正常的学生有900人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
分数段
频数
频率
80≤x<85
x
0.2
85≤x<90
80
y
90≤x<95
60
0.3
95≤x<100
20
0.1
根据以上图表提供的信息,解答下列问题:
(1)写出表中x,y的数值;
(2)请补全频数分布直方图;
(3)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(4)获奖成绩的中位数落在哪个分数段?
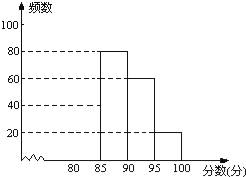
-
科目: 来源: 题型:
查看答案和解析>>【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,小明从中随机地抽取一张,把卡片上的数字做为被减数,将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,小华从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小明与小华做游戏,规则是:若这两数的差为非负数,则小明赢;否则,小华赢.你认为该游戏公平吗?请说明理由.如果不公平,请你修改游戏规则,使游戏公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=
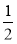 ,求AC的长.
,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为

(1)求证:无论
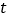 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;(2)①当
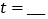 s时,CE⊥AD;
s时,CE⊥AD;②当
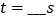 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.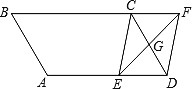
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
30
45
租金(元/辆)
450
600
已知某中学计划租用
 两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.
两种型号的客车共10辆送七年级师生去某地参加社会实践活动,已知该中学租车的总费用不超过5600元.(1)求最多能租用多少辆B型号客车?
(2)若七年级师生共有380人,请写出所有可能的租车方案.
相关试题

