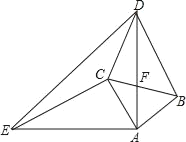
【题目】如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC=2![]() ,求∠ACD的度数;
,求∠ACD的度数;
(3)在(2)的条件下,直接写出DE的长为 .(只填结果,不用写计算过程)
参考答案:
【答案】(1)证明见解析;(2)∠ACD=135°;(3)2![]() .
.
【解析】
(1)根据等腰直角三角形的性质可以得出∠EAC=∠DAB,再有AB=AC,AD=AE,根据SAS就可以得出结论;
(2)根据勾股定理可以求出BC的值为2![]() ,就可以得出BC=DC,在△BCD中由勾股定理的逆定理可以得出△BCD为等腰直角三角形,就可以得出∠BCD=90°,从而得出∠ACD的度数;
,就可以得出BC=DC,在△BCD中由勾股定理的逆定理可以得出△BCD为等腰直角三角形,就可以得出∠BCD=90°,从而得出∠ACD的度数;
(3)由(2)可以知道∠CDB=45°,而∠ABC=45°,就可以得出△ABD是直角三角形,由勾股定理就可以求出AB的值,再由勾股定理就可以求出DE的值.
解:(1)∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠EAC=∠BAD.
在△ACE和△ABD中,
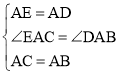 ,
,
∴△ACE≌△ABD(SAS);
(2)∵△ACE≌△ABD(SAS),
∴DB=EC=4,
在Rt△ABC中,AB2+AC2=BC2,
∴BC2=22+22=8,
在△DBC中,BC2+DC2=8+8=16=42=BD2,
∴∠DCB=90°,
∴∠ACD=90°+45°=135°;
(3)∵BC2=8,DC2=8,
∴BC=DC.
∵∠DCB=90°,
∴∠DBC=45°.
∵∠ABC=45°,
∴∠ABD=90°.
在Rt△ABD中由勾股定理,得:
![]() .
.
在Rt△AED中由勾股定理,得:
![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
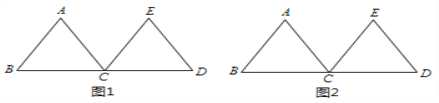
查看答案和解析>>【题目】如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画一个直角三角形; (2)在图2中画出∠ACE的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=OC,则四边形ABCD是什么特殊四边形?请直接给出你的结论,不必证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有四把不同的钥匙和两把不同的锁,其中有两把钥匙可以分别打开这两把锁,另两把钥匙是打不开此两把锁的,现随意取出一把钥匙去开其中一把锁.
(1)请用画树状图的方法表示所有可能结果;
(2)求小明一次打开锁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点
所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点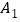 、
、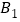 、
、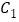 ,再连接
,再连接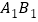 、
、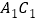 、
、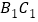 得到
得到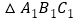 ,则下列说法不正确的是( )
,则下列说法不正确的是( )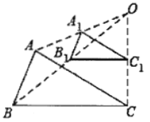
A.
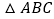 与
与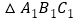 是位似图形
是位似图形B.
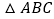 与是
与是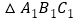 相似图形
相似图形C.
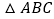 与
与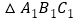 的周长比为2:1
的周长比为2:1D.
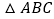 与
与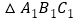 的面积比为2:1
的面积比为2:1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示.若座板CD平行于地面,前支撑架AB与后支撑架OF分别与CD交于点E、D,ED= 15㎝,OD=20㎝,DF=40㎝,∠ODC=60°,∠AED=50°.
(1)求两支架着地点B、F之间的距离;
(2)若A、D两点所在的直线正好与地面垂直,求椅子的高度(结果取整数).
(参考数据:
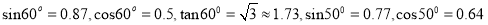
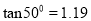 ;可使用科学计算器.)
;可使用科学计算器.)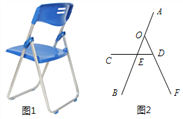
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数28、29.4、31.9、27、28.8、34.1、29.4的中位数、众数、极差分别是( )
A.
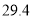 、
、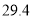 、
、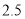 B.
B. 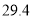 、
、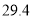 、
、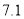
C. 27、29、
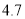 D.
D.  、28、
、28、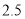
相关试题

