【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=OC,则四边形ABCD是什么特殊四边形?请直接给出你的结论,不必证明.

参考答案:
【答案】(1)详见解析;(2)若OD=OC,则四边形ABCD是矩形.
【解析】试题分析:(1)根据平行线的性质证明∠DFO=∠BEO,由O为AC的中点和AE=CF,证明OE=OF,根据ASA即可证得;
(2)根据全等三角形的性质,证明OB=OD,根据对角线互相平分且相等的四边形是矩形即可得证.
(1)证明:∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,即OA=OC,AE=CF,
∴OA﹣AE=OC﹣CF,即OE=OF,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(AAS);
(2)若OD=OC,则四边形ABCD是矩形.
理由是:∵△BOE≌△DOF,
∴OB=OD,
又∵OA=OC,OD=OC,
∴OA=OC= OB=OD,
∴四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017南宁,第26题,10分)如图,已知抛物线
 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,
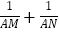 均为定值,并求出该定值.
均为定值,并求出该定值.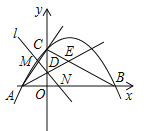
-
科目: 来源: 题型:
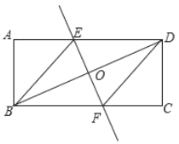
查看答案和解析>>【题目】如图,直线经过矩形
 的对角线
的对角线 的中点
的中点 ,分别与矩形的两边相交于点
,分别与矩形的两边相交于点 、
、 .
.
(1)求证:
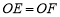 ;
;(2)若
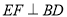 ,则四边形
,则四边形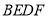 是______形,并说明理由;
是______形,并说明理由;(3)在(2)的条件下,若
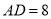 ,
,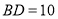 ,求
,求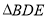 的面积.
的面积. -
科目: 来源: 题型:
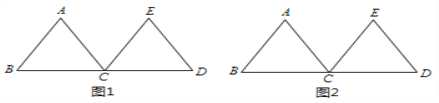
查看答案和解析>>【题目】如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画一个直角三角形; (2)在图2中画出∠ACE的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有四把不同的钥匙和两把不同的锁,其中有两把钥匙可以分别打开这两把锁,另两把钥匙是打不开此两把锁的,现随意取出一把钥匙去开其中一把锁.
(1)请用画树状图的方法表示所有可能结果;
(2)求小明一次打开锁的概率.
-
科目: 来源: 题型:
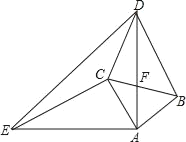
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC=2
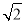 ,求∠ACD的度数;
,求∠ACD的度数;(3)在(2)的条件下,直接写出DE的长为 .(只填结果,不用写计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
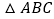 所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点
所在平面上任意取一点O(与A、B、C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点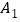 、
、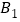 、
、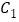 ,再连接
,再连接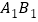 、
、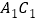 、
、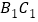 得到
得到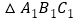 ,则下列说法不正确的是( )
,则下列说法不正确的是( )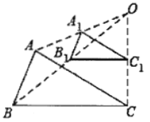
A.
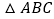 与
与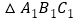 是位似图形
是位似图形B.
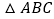 与是
与是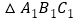 相似图形
相似图形C.
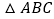 与
与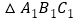 的周长比为2:1
的周长比为2:1D.
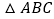 与
与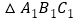 的面积比为2:1
的面积比为2:1
相关试题

