【题目】如图1,将一块含![]() 角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中
角的三角板ABO的一边BO放在直线MN上,AB边在直线MN的上方,其中![]() ,另一块含
,另一块含![]() 角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.
角的三角板POQ的一边OQ在直线MN上,另一边OP在直线MN的下方.

![]() 现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为
现将图1中的三角板POQ绕点O按顺时针方向旋转,当直线MN恰好为![]() 的平分线时,如图2所示,则
的平分线时,如图2所示,则![]() 的度数______度;
的度数______度;
![]() 继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在
继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置,使得边OA落在![]() 的内部,且AO恰好为
的内部,且AO恰好为![]() 的平分线时,求
的平分线时,求![]() 的度数;
的度数;
![]() 在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒
在上述直角三角板从图1按顺时针方向旋转至图位置为止,这个过程中,若三角板POQ绕点O以每秒![]() 的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分
的速度匀速旋转,当三角板POQ的OP边或OQ边所在直线平分![]() ,则求此时三角板POQ绕点O旋转的时间t的值
,则求此时三角板POQ绕点O旋转的时间t的值![]() 请直接写出答案
请直接写出答案![]() .
.
参考答案:
【答案】(1)75;(2)![]() ;(3)当OP边所在直线平分
;(3)当OP边所在直线平分![]() 时旋转时间为5秒或17秒,当OQ边所在直线平分
时旋转时间为5秒或17秒,当OQ边所在直线平分![]() 时旋转时间为11秒或23秒.
时旋转时间为11秒或23秒.
【解析】
(1)根据三角板PQO的特性结合题意可得出∠POM=45°,在平角MON中可求出∠AOP的度数;
(2)根据角平分线的定义即可得到结论;
(3)此题分两种情况,一种OP边所在直线平分∠AOB,另一种OQ边所在直线平分∠AOB,找出两种情况下三角板PQO绕点O旋转的度数,即可求出时间t.
解:![]() 直线MN平分
直线MN平分![]() ,
,![]() ,
,
![]() ,
,
又![]() 且
且![]() 为平角,
为平角,
![]() ,
,
故![]() 的度数为
的度数为![]() ;
;
故答案为:75;
![]() 恰好为
恰好为![]() 的平分线,
的平分线,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 根据题意可知,分两种情况,
根据题意可知,分两种情况,
![]() 当OP边所在直线平分
当OP边所在直线平分![]() 时,三角板PQO绕点O旋转的度数为
时,三角板PQO绕点O旋转的度数为![]() 或
或![]() ,
,
![]() ,
,
![]() 时间
时间![]() 秒
秒![]() 或
或![]() 秒
秒![]() ;
;
![]() 当OQ边所在直线平分
当OQ边所在直线平分![]() 时,三角板PQO绕点O旋转的度数为
时,三角板PQO绕点O旋转的度数为![]() 或
或![]() ,
,
![]() ,
,
![]() 时间
时间![]() 秒
秒![]() 或
或![]() 秒
秒![]() .
.
综合![]() 得当OP边所在直线平分
得当OP边所在直线平分![]() 时旋转时间为5秒或17秒,当OQ边所在直线平分
时旋转时间为5秒或17秒,当OQ边所在直线平分![]() 时旋转时间为11秒或23秒.
时旋转时间为11秒或23秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题:
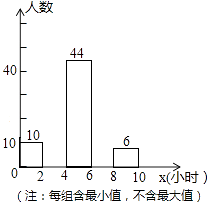
(1)本次调查属于调查,样本容量是;
(2)请补全频数分布直方图中空缺的部分;
(3)若从这100名学生中随机抽取1名学生,求抽取的这个学生每周去图书馆的时间恰好在8﹣10小时的概率;
(4)估计全校学生每周去图书馆的时间不少于6小时的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
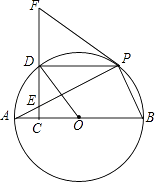
(1)证明:FP是⊙O的切线;
(2)若四边形OBPD是菱形,证明:FD=ED. -
科目: 来源: 题型:
查看答案和解析>>【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为
 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM= EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=
 ,求乙的游泳速度.
,求乙的游泳速度. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产一种工具,据市场调查,若按每个工具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个工具的固定成本Q(元)与月销售y(个)满足如下关系:
月销量y(个)
100
160
240
320
每个工具的固定成本Q(元)
96
60
40
30
(1)写出月产销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
相关试题

