搜索
【题目】（1）把数轴补充完整．
（2）在数轴上表示下列各数．
（3）用“＜”连接起来． ．
（4）﹣|﹣2|与﹣4之间的距离是 ．
3
，﹣4，﹣（﹣1.5），﹣|﹣2|
参考答案：
【答案】（1）见解析；（2）见解析；（3）﹣4＜﹣|﹣2|＜﹣（﹣1.5）＜3
；（4）2
【解析】
（1）把数轴补充完整即可；
（2）在数轴上表示出各数即可；
（3）根据数轴上的点表示的数右边的总比左边的大，可得答案；
（4）观察数轴可得结果．
解：（1）把数轴补充完整如图：
（2）﹣（﹣1.5）＝1.5，﹣|﹣2|＝﹣2，
在数轴上表示出各数如图：
（3）它们的大小关系为﹣4＜﹣|﹣2|＜﹣（﹣1.5）＜3．
故答案为：﹣4＜﹣|﹣2|＜﹣（﹣1.5）＜3；
（4）从数轴可知：﹣|﹣2|与﹣4之间的距离是2．
故答案为：2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当k，m分别为何值时，关于x，y的方程组
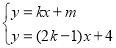至少有一组解? -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OE=OF；
（2）若CE=12，CF=5，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．
（1）猜想四边形EFGH的形状，直接回答，不必说明理由；
（2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；
（3）如果（2）中，∠APC=∠BPD=90°，其他条件不变，先补全图3，再判断四边形EFGH的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数：
﹣3.1，3.1415，﹣
，+31，0.618，﹣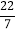
，0，﹣1，﹣（﹣3），填在相应的集合里分数集合： ；
整数集合： ；
非负整数集合： ；
正有理数集合： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点E，则DF的长为（ ）
A. 4.5 B. 5 C. 5.5 D. 6
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读，再解答．
我们在判断点(－7，20)是否在直线y＝2x＋6上时，常用的方法是：把x＝－7代入y＝2x＋6中，由2×(－7)＋6＝－8≠20，判断出点(－7，20)不在直线y＝2x＋6上．小明由此方法并根据“两点确定一条直线”，推断出点A(1，2)，B(3，4)，C(－1，6)三点可以确定一个圆，你认为他的推断正确吗?请你利用上述方法说明理由．
相关试题
