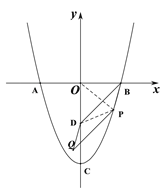
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
参考答案:
【答案】(1)①抛物线解析式为y=x2﹣4;②0<S四边形BDQP≤![]() ;(2)
;(2)![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】试题分析:(1)①把 A(-2,0),C(0,-4)代入![]() ,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(
,求得a、c的值,即可得抛物线的解析式;②连接DB、OP,设P(![]() ,
, ![]() ),因A(-2,0),对称轴为
),因A(-2,0),对称轴为![]() 轴,可得B(2,0),即可得
轴,可得B(2,0),即可得![]()
![]()
![]() ,再由点P在第四象限运动,可得x单位取值范围
,再由点P在第四象限运动,可得x单位取值范围![]() ,由抛物线的图象即可得△BDP的取值范围为
,由抛物线的图象即可得△BDP的取值范围为![]() ,因
,因![]() 即可得平行四边形BDQP面积的取值范围为
即可得平行四边形BDQP面积的取值范围为![]() ;(2)过点P作PG⊥AB,设A(
;(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() ),由PG∥
),由PG∥![]() 轴,根据相似三角形的判定方法可得
轴,根据相似三角形的判定方法可得![]() ,
, ![]() ,再由相似三角形的性质可得
,再由相似三角形的性质可得![]() ,
, ![]() ,代入数值可得
,代入数值可得![]() ,
, ![]() ,把这两个式子相加可得
,把这两个式子相加可得![]() ,令
,令![]() ,即可得
,即可得![]() ,
, ![]() ,所以
,所以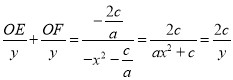 ,即
,即![]() ,所以
,所以![]() ,即可得
,即可得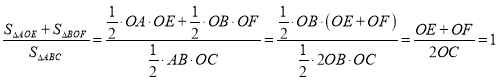
所以可得结论![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
试题解析:
(1)①![]()
②连接DB、OP,设P(![]() ,
, ![]() )
)
∵A(-2,0),对称轴为![]() 轴
轴
∴B(2,0)
∴![]()
![]()
![]()
![]()
∵点P在第四象限运动
∴![]()
∴由抛物线的图象可得: ![]()
∵![]() ∴
∴![]()
(2)过点P作PG⊥AB,设A(![]() ,0),B(
,0),B(![]() ,0),P(
,0),P(![]() ,
, ![]() )
)

∴PG∥![]() 轴
轴
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵当![]() 时,∴
时,∴![]() ,即
,即![]() ,
, ![]()
∴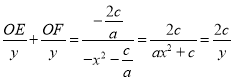
∴![]() ∴
∴![]()
∴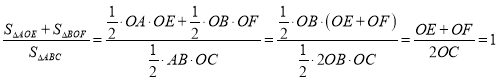
∴![]() 与
与![]() 、
、![]() 无关,比值为1.
无关,比值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2﹣(﹣18)+(﹣7)﹣15
(2)(﹣48)÷8﹣(﹣25)×(﹣6)
(3)﹣14﹣|2﹣5|+6×(﹣ )
)
(4)﹣36×( ﹣
﹣  ﹣
﹣ 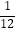 )÷(﹣2)
)÷(﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π)

(1)图中阴影部分的周长为cm.
(2)图中阴影部分的面积为cm2 .
(3)当a=4时,求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为100元,出售时标价为150元,后来由于该商品积压,商店准备打折出售,但要保证利润不低于20%,则最多可打( )
A. 6折 B. 7折 C. 8折 D. 9折
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=
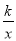 (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
A.(﹣1,2)
B.(﹣1,﹣1)
C.(﹣1,1)
D.(1,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+2x﹣2的图象的顶点坐标是( )
A.(2,﹣2)
B.(1,﹣2)
C.(1,﹣3)
D.(﹣1,﹣3)
相关试题

