搜索
【题目】抛物线y=x2+2x﹣2的图象的顶点坐标是（ ）
A.（2，﹣2）
B.（1，﹣2）
C.（1，﹣3）
D.（﹣1，﹣3）
参考答案：
【答案】D
【解析】解：
∵y=x2+2x﹣2=（x+1）2﹣3，
∴抛物线顶点坐标为（﹣1，﹣3），
故选D．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=ax2+c与x轴交于A、B两点（A在B的左边），与y轴交于点C，抛物线上有一动点P
（1）若A（﹣2，0），C（0，﹣4）
①求抛物线的解析式；
②在①的情况下，若点P在第四象限运动，点D（0，﹣2），以BD、BP为邻边作平行四边形BDQP，求平行四边形BDQP面积的取值范围．
（2）若点P在第一象限运动，且a＜0，连接AP、BP分别交y轴于点E、F，则问
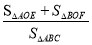是否与a，c有关？若有关，用a，c表示该比值；若无关，求出该比值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数y1=ax+b（a≠0）的图象与y轴相交于点A，与反比例函数y2=
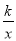（c≠0）的图象相交于点B（3，2）、C（﹣1，n）．（1）求一次函数和反比例函数的解析式；
（2）根据图象，直接写出y1＞y2时x的取值范围；
（3）在y轴上是否存在点P，使△PAB为直角三角形？如果存在，请求点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果点M在y轴的左侧，且在x轴的上侧，到两坐标轴的距离都是1，则点M的坐标为（ ）
A.（﹣1，2）
B.（﹣1，﹣1）
C.（﹣1，1）
D.（1，1） -
科目： 来源： 题型：
查看答案和解析>>【题目】记M（1）=﹣2，M（2）=（﹣2）×（﹣2），M（3）=（﹣2）×（﹣2）×（﹣2），…，M（n）=
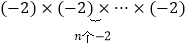
（1）填空：M（5）= ， M（50） 是一个数（填“正”或“负”）
（2）计算：①2M（6）+M（7）；②4M（7）+2M（8）；
（3）直接写出2016M（n）+1008M（n+1）的值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】函数y=mxm-1+（m-1）是一次函数，则（ ）
A. m≠0 B. m=2 C. m=2或4 D. m＞2
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据给出的数轴及已知条件，解答下面的问题：
（1）已知点A，B，C表示的数分别为1，﹣
，﹣3观察数轴，与点A的距离为3的点表示的数是 ， B，C两点之间的距离为；
（2）若将数轴折叠，使得A点与C点重合，则与B点重合的点表示的数是；若此数轴上M，N两点之间的距离为2015（M在N的左侧），且当A点与C点重合时，M点与N点也恰好重合，则M，N两点表示的数分别是：M ， N；
（3）若数轴上P，Q两点间的距离为m（P在Q左侧），表示数n的点到P，Q两点的距离相等，则将数轴折叠，使得P点与Q点重合时，P，Q两点表示的数分别为：P ， Q（用含m，n的式子表示这两个数）．
相关试题
