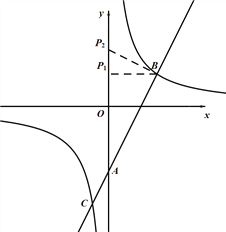
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(c≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围;
(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)反比例函数解析式为: ![]() ,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0,
,一次函数解析式为y1=2x﹣4;(2)由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3;(3)y轴上存在点P,使△PAB为直角三角形,P1(0,2)、P2(0, ![]() ).
).
【解析】试题分析:(1) 把B(3,2)代入![]() 求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)
求得k的值,即可得反比例函数解析式,把C(-1,n)代入反比例函数的解析式,求得n值,再利用待定系数法求一次函数的解析式即可;(2)观察图象,直接写出结论即可;(3)![]() 轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
轴上存在点P,使△PAB为直角三角形,分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
试题解析:
(1)把B(3,2)代入![]() 得:
得: ![]() =6
=6
∴反比例函数解析式为: ![]()
把C(-1,n)代入![]() ,得:n=-6
,得:n=-6
∴C(-1,-6)
把B(3,2)、C(-1,-6)分别代入![]() ,得:
,得:
![]() ,解得:
,解得: ![]()
所以一次函数解析式为![]()
(2)由图可知,当写出![]() >
>![]() 时
时![]() 的取值范围是-1<
的取值范围是-1<![]() <0或者
<0或者![]() >3
>3
(3)![]() 轴上存在点P,使△PAB为直角三角形
轴上存在点P,使△PAB为直角三角形
过B作BP1⊥![]() 轴于P1
轴于P1
∠B P1 A=90°,△P1AB为直角三角形
此时,P1(0,2)
过B作BP2⊥AB交![]() 轴于P2
轴于P2
∠P2 BA=90°,△P2 AB为直角三角形
在Rt△P1AB中,
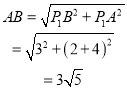
在Rt△P1 AB和Rt△P2 AB
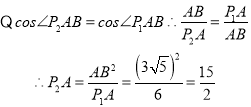
∴![]()
∴P2(0, ![]() )
)
综上所述,P1(0,2)、P2(0, ![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π)

(1)图中阴影部分的周长为cm.
(2)图中阴影部分的面积为cm2 .
(3)当a=4时,求出阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为100元,出售时标价为150元,后来由于该商品积压,商店准备打折出售,但要保证利润不低于20%,则最多可打( )
A. 6折 B. 7折 C. 8折 D. 9折
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问
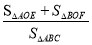 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
A.(﹣1,2)
B.(﹣1,﹣1)
C.(﹣1,1)
D.(1,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+2x﹣2的图象的顶点坐标是( )
A.(2,﹣2)
B.(1,﹣2)
C.(1,﹣3)
D.(﹣1,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】记M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,M(n)=
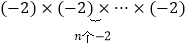
(1)填空:M(5)= , M(50) 是一个数(填“正”或“负”)
(2)计算:①2M(6)+M(7);②4M(7)+2M(8);
(3)直接写出2016M(n)+1008M(n+1)的值为 .
相关试题

