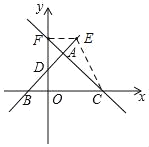
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.

参考答案:
【答案】(1)y=x+1;(2)△ABC是等腰直角三角形;(3)存在,点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.
【解析】
(1)利用待定系数法,即可得到直线AD的解析式;
(2)依据点的坐标求得AB=2![]() ,AC=2
,AC=2![]() ,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
,BC=4,即可得到AB2+AC2=16=BC2,进而得出△ABC是等腰直角三角形;
(3)依据4S△BOD=S△ACE,即可得到AE=![]() ,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=
,分两种情况进行讨论:①点E在直线AC的右侧,②点E在直线AC的左侧,分别依据AD=AE=![]() ,即可得到点E的坐标.
,即可得到点E的坐标.
解:(1)直线AD的解析式为y=kx+b,
∵直线AD经过点A(1,2),点D(0,1),
∴![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1;
(2)∵y=x+1中,当y=0时,x=﹣1;y=﹣x+3中,当y=0时,x=3,
∴直线AD与x轴交于B(﹣1,0),直线AC与x轴交于C(3,0),
∵点A(1,2),
∴AB=2![]() ,AC=2
,AC=2![]() ,BC=4,
,BC=4,
∵AB2+AC2=16=BC2,
∴∠BAC=90°,
∴△ABC是等腰直角三角形;
(3)存在,
AC=2![]() ,S△BOD=
,S△BOD=![]() ×1×1=
×1×1=![]() ,
,
∵△ABC是等腰直角三角形,
∴∠CAE=90°,
∵S△ACE=![]() AE×AC,4S△BOD=S△ACE,
AE×AC,4S△BOD=S△ACE,
∴4×![]() =
=![]() ×AE×2
×AE×2![]() ,
,
解得AE=![]() ,
,
①如图,当点E在直线AC的右侧时,过E作EF⊥y轴于F,
∵AD=AE=![]() ,∠EDF=45°,
,∠EDF=45°,
∴EF=DF=2,OF=2+1=3,
∴E(2,3);
②当点E在直线AC的左侧时,
∵AD=AE=![]() ,
,
∴点E与点D重合,即E(0,1),
综上所述,当点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
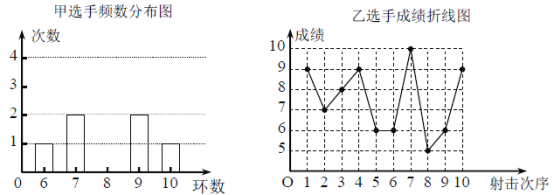
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手
平均数
中位数
众数
方差
甲

8
8
c
乙
7. 5
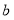
6和9
2. 65
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求
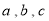 的值;
的值;(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店为了鼓励营业员多销售服装,在原来的支付月薪方式(y1):每月底薪600元,每售出一件服装另支付4元的提成,推出第二种支付月薪的方式(y2),如图所示,设x(件)是一个月内营业员销售服装的数量,y(元)是营业员收入的月薪,请结合图形解答下列问题:
(1)求y1与y2的函数关系式;
(2)该服装店新推出的第二种付薪方式是怎样向营业员支付薪水的?
(3)如果你是营业员,你会如何选择支付薪水的方式?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
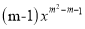 是反比例函数.
是反比例函数.(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(
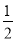 ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°.(1)求∠A的度数;(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=4
 ,求图中阴影部分的面积.(结果保留π)
,求图中阴影部分的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:
探究函数
 的图象与性质.
的图象与性质. 小东根据学习函数的经验,对函数
 的图象与性质进行了探究.
的图象与性质进行了探究. 下面是小东的探究过程,请补充完成:
(1)填表

…

0
1
2
3
4
5
6
. . .

…
3
2


. . .
(2)根据(1)中的结果,请在所给坐标系中画出函数
 的图象;
的图象;(3)结合函数图象,请写出该函数的一条性质. 
相关试题

