【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
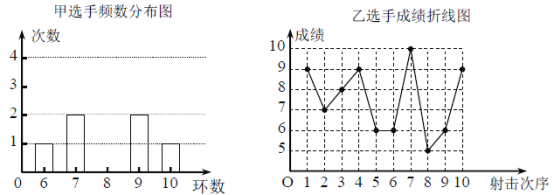
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手 | 平均数 | 中位数 | 众数 | 方差 |
甲 |
| 8 | 8 | c |
乙 | 7. 5 |
| 6和9 | 2. 65 |
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求![]() 的值;
的值;
(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
参考答案:
【答案】(1)4,图见解析;(2)8、1.2、7.5;(3)从平均数看,甲成绩优于乙的成绩;从方差看,甲的方差小,说明甲的成绩稳定
【解析】
(1)根据甲成绩的众数求解可得;
(2)根据平均数、方差和中位数的定义逐一计算可得;
(3)根据平均数和方差的意义求解可得.
(1)甲选手命中8环的次数为10-(1+2+2+1)=4,
补全图形如下:

(2)a=![]() =8(环),
=8(环),
c=![]() ×[(6-8)2+2×(7-8)2+4×(8-8)2+2×(9-8)2+(10-8)2]=1.2,
×[(6-8)2+2×(7-8)2+4×(8-8)2+2×(9-8)2+(10-8)2]=1.2,
b=![]() =7.5,
=7.5,
(3)从平均数看,甲成绩优于乙的成绩;
从方差看,甲的方差小,说明甲的成绩稳定.
-
科目: 来源: 题型:
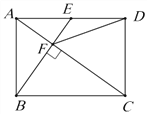
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,下列四个结论:①△AEF∽△CAB ;②
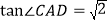 ;③DF=DC; ④CF=2AF.
;③DF=DC; ④CF=2AF.其中正确的结论是________________(填番号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图
 ,
,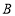 分别为数轴上的两点,
分别为数轴上的两点,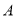 点对应的数为-10,
点对应的数为-10,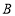 点对应的数为90.
点对应的数为90.
(1)
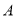 ,
,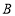 两点间的距离为________.
两点间的距离为________.(2)现在有一只电子蚂蚁
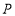 从
从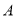 点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁
点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁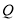 恰好从
恰好从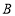 点出发,以3个单位/秒的速度向左运动.运动时间为
点出发,以3个单位/秒的速度向左运动.运动时间为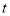 秒,用含
秒,用含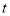 的代数式表示:
的代数式表示:①点
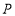 在数轴上表示的数为________.
在数轴上表示的数为________.②若两只电子蚂蚁在数轴上的
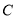 点相遇,则
点相遇,则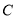 点对应的数是多少.
点对应的数是多少.(3)若当电子蚂蚁
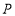 从
从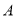 点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁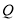 恰好从
恰好从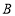 点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度.
点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店为了鼓励营业员多销售服装,在原来的支付月薪方式(y1):每月底薪600元,每售出一件服装另支付4元的提成,推出第二种支付月薪的方式(y2),如图所示,设x(件)是一个月内营业员销售服装的数量,y(元)是营业员收入的月薪,请结合图形解答下列问题:
(1)求y1与y2的函数关系式;
(2)该服装店新推出的第二种付薪方式是怎样向营业员支付薪水的?
(3)如果你是营业员,你会如何选择支付薪水的方式?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
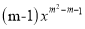 是反比例函数.
是反比例函数.(1)求m的值;
(2)指出该函数图象所在的象限,在每个象限内,y随x的增大如何变化?
(3)判断点(
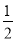 ,2)是否在这个函数的图象上.
,2)是否在这个函数的图象上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.

相关试题

