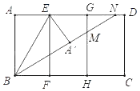
【题目】如图,矩形纸片ABCD,AB=8,AE=EG=GD=4,AB∥EF∥GH.将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH,AD分别交于点M,N,然后将纸片展开.
(1)连接EM,证明A′M=MG;
(2)设A′M=MG=x,求x值.
参考答案:
【答案】(1)见解析;(2)A′M=6﹣2![]() .
.
【解析】
(1)由翻折的性质得到A'E=EG,由矩形的性质好而其他条件得∠EGM=90°,从而得到Rt△EA'M≌Rt△EGM(HL),则A′M=MG;
(2)由已知条件,根据勾股定理得到BE的值,再由已知条件得到![]() ,设A′M=MG=x,从而得到x的值.
,设A′M=MG=x,从而得到x的值.
(1)连接EM,如图.
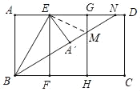
由折叠可知EA=EA',
∵AE=EG,∠EA'B=∠A=90°
∴A'E=EG,
∵四边形ABCD为矩形,AB∥EF∥GH,
∴∠EGM=90°
∴∠EGM=∠EA'M,
∴Rt△EA'M≌Rt△EGM(HL),
∴A′M=MG;
(2)∵AB=8,AE=4,
∴BE=![]() ,
,
∴EN=BE=![]() ,
,
∵AB∥EF∥GH,AE=EG=GD=4,AB=8,
∴![]() ,
,
设A′M=MG=x,
![]()
x=6﹣2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,四个顶点坐标分别为A(m,n),B(1,2),C(m+
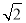 ﹣1,2),D(m+
﹣1,2),D(m+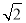 ,n).求m,n的值.
,n).求m,n的值.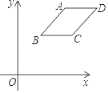
-
科目: 来源: 题型:
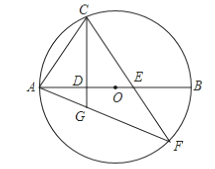
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于点D,E是AB上一点,直线CE与⊙O交于点F,连结AF,与直线CD交于点G.
求证:(1)∠ACD=∠F; (2)AC2=AG·AF.
-
科目: 来源: 题型:
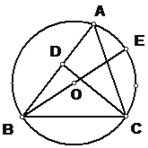
查看答案和解析>>【题目】已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)已知CD=6、AD=3、BD=8,求⊙O的直径BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表
售价x(单位:元/千克)
30
25
20
每天销售量y(单位:千克)
5
55
105
如果已知草莓每天销量y与售价x(30.5>x>14)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克,哪天的销售利润更高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,
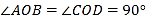 ,
,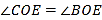 ,点
,点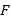 为
为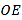 反向延长线上一点(图中所有角均指小于
反向延长线上一点(图中所有角均指小于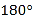 的角).下列结论:①
的角).下列结论:①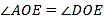 ;②
;②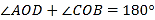 ;③
;③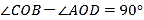 ;④
;④ .其中正.确.结论的个数有( ).
.其中正.确.结论的个数有( ).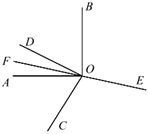
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“禁毒知识竞赛”,从中抽取了部分学生,将他们的竞赛成绩进行统计后分为
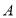 ,
,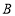 ,
,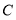 ,
,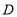 四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题:
四个等次,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题: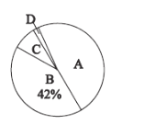
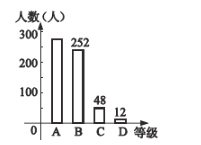
(1)抽取了_______名学生成绩;
(2)扇形统计图中
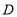 等级所在扇形的圆心角度数是_________;
等级所在扇形的圆心角度数是_________;(3)为估算全校八年级“禁毒知识竞赛”平均分,现将
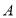 、
、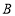 、
、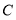 、
、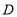 依次记作
依次记作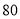 分、
分、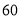 分、
分、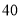 分、
分、 分,请估算该校八年级知识竞赛平均分.
分,请估算该校八年级知识竞赛平均分.
相关试题

