【题目】如图，若反比例函数y=﹣与一次函数y=mx﹣2的图象都经过点A（a，2）

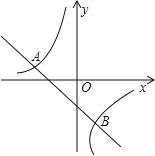
（1）求A点的坐标及一次函数的解析式；

（2）设一次函数与反比例函数图象的另一交点为B，求B点坐标，并利用函数图象写出使一次函数的值小于反比例函数的值的x的取值范围．

参考答案：

【答案】（1）y=﹣x﹣2；（2）﹣4＜x＜0或x＞2

【解析】解：（1）把y=2代入反比例函数y=﹣

∴x=﹣4，

∴A（﹣4，2）．

把A（﹣4，2）代入一次函数y=mx﹣2

解得m=﹣1

∴一次函数y=mx﹣2为y=﹣x﹣2．

（2）根据题意把反比例函数y=﹣代入一次函数y=﹣x﹣2

∴和

∴B（2，﹣4）

利用函数图象可得使一次函数的值小于反比例函数的值的x的取值范围是﹣4＜x＜0或x＞2．

关闭