【题目】如图,正方形纸片ABCD的边长为4cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是____.

参考答案:
【答案】2
【解析】分析:
如下图所示,设AB、CD的中点分别为K、G,连接KG、BD相交于点O,则由题意可知当点E与点B重合时,点Q与点O重合,当点E与点C重合时,点Q与点G重合,即点Q的运动路线是线段OG,根据题中已知条件求出线段OG的长度即可.
详解:如下图,设AB、CD的中点分别为K、G,连接KG、BD相交于点O,
∵当点E与点B重合时,由题意可知此时点Q与点O重合;而当点E与点C重合时,由题意可知此时点Q与点G重合,
∴随着点M的移动,点Q的移动路线是线段OG,
∵由折叠的性质可知:BO=DO,DG=CG,
∴线段OG是△DBC的中位线,
∴OG=![]() BC=
BC=![]() .
.
故答案为:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ACB=90
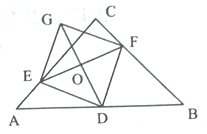
 ,AC=BC=4,D为AB的中点,E,F分别是AC, BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD.连接DE, GE, GF.
,AC=BC=4,D为AB的中点,E,F分别是AC, BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD.连接DE, GE, GF.(1)求证:四边形EDFG是正方形;
(2)直接写出四边形EDFG面积的最小值和E点所在的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华联超市购进一批四阶魔方,按进价提高40%后标价,为了让利于民,增加销量,超市决定打八折出售,这时每个魔方的售价为28元.
(1)求魔方的进价?
(2)超市卖出一半后,正好赶上双十一促销,商店决定将剩下的魔方以每3个80元的价格出售,很快销售一空,这批魔方超市共获利2800元,求该超市共购进魔方多少个?
-
科目: 来源: 题型:
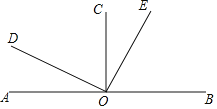
查看答案和解析>>【题目】如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE=
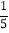 ∠BOD.
∠BOD.(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.

(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 , 衍生直线的解析式是;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题一:如图1,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地,若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h), 两车之间距离为y(km).
(1)当甲追上乙时,x=_________.
(2)请用x的代数式表示y.

问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动_______km;时针OE指向圆周上的点的速度为每分钟转动_______km.
(2)若从2:00起计时,求几分钟后分针与时针第一次重合?

相关试题

