【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0.
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)当Rt△ABC的斜边长a为![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长.
,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长.
参考答案:
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)根据方程的系数结合根的判别式,可得出△=(2k-3)2+4>0,由此可证出:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)根据根与系数的关系结合勾股定理,即可得出关于k的一元二次方程,解之即可得出k值,进而可得出原方程,再根据根与系数的关系,即可求出△ABC的周长.
试题解析:解:(1)△=[﹣(2k+1)]2﹣4(4k﹣3)=4k2﹣12k+13=(2k﹣3)2+4.
∵(2k﹣3)2≥0,∴(2k﹣3)2+4>0,即△>0,∴无论k取什么实数值,该方程总有两个不相等的实数根;
(2)∵b、c是方程x2﹣(2k+1)x+4k﹣3=0的两个根,∴b+c=2k+1,bc=4k﹣3.
∵a2=b2+c2,a=![]() ,∴k2﹣k﹣6=0,∴k1=3,k2=﹣2.
,∴k2﹣k﹣6=0,∴k1=3,k2=﹣2.
∵b、c均为正数,∴4k﹣3>0,∴k=3,此时原方程为x2﹣7x+9=0,∴b+c=7,∴△ABC的周长为7+ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题(1)-100 + 80;
(2)(-18)÷4;
(3)
 ;
;(4)﹣7.2﹣0.8﹣5.6+11.6
(5)
 ;
;(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,在数轴上,|a|表示数a到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a,b表示,那么A、B两点之间的距离为:AB=|a-b|.利用此结论,回答以下问题:
(1)数轴上表示2和5的两点的距离是 ,数轴上表示-20和-5的两点之间的距离是 ,数轴上表示15和-30的两点之间的距离是 .
(2)数轴上表示x和-1的两点A,B之间的距离是 ,如果|AB|=2,那么x是
(3)式子|x+1|+|x-2|+|x-3|的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并回答问题:
三峡之最
三峡工程是中国,也是世界上最大的水利枢纽工程,是治理和开发长江的关键性骨干工程.它具有防洪、发电、航运等综合效益.
三峡水库总库容
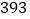 亿立方米,防洪库容
亿立方米,防洪库容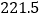 亿立方米,水库调洪可消减洪峰流量达每秒
亿立方米,水库调洪可消减洪峰流量达每秒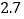 ─
─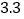 万立方米,是世界上防洪效益最为显著的水利工程.
万立方米,是世界上防洪效益最为显著的水利工程.三峡水电站总装机
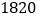 万千瓦,年发电量
万千瓦,年发电量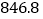 亿千瓦.时,是世界上最大的电站.
亿千瓦.时,是世界上最大的电站.三峡水库回水可改善川江
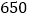 公里的航道,使宜渝船队吨位由现在的
公里的航道,使宜渝船队吨位由现在的 吨级堤高到万吨级,年单向通过能力由
吨级堤高到万吨级,年单向通过能力由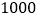 万吨增加到
万吨增加到 万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.
万吨;宜昌以下长江枯水航深通过水库调节也有所增加,是世界上航运效益最为显著的水利工程.思考:
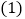 三峡水电站年发电量
三峡水电站年发电量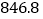 亿千瓦.时,一个普通家庭一天用电
亿千瓦.时,一个普通家庭一天用电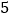 千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留
千瓦.时,三峡水电站可同时供多少普通家庭一年的用电?(保留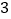 个有效数字)
个有效数字) 宜都市
宜都市 万人,平均一户
万人,平均一户 个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数).
个人,三峡水电站一年可同时供多少个像宜都市这样的城市的用电?(结果保留整数). -
科目: 来源: 题型:
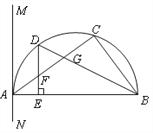
查看答案和解析>>【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出图中的立体图形的名称.

①_______;②_______;③_______;④_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2
 cmB.3
cmB.3 cmC.4
cmC.4 cmD.3cm
cmD.3cm
相关试题

