【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
参考答案:
【答案】A
【解析】
过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,然后利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△EDF=S△GDH,设面积为S,然后根据S△ADF=S△ADH列出方程求解即可.
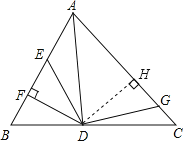 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,![]() ,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即38+S=50-S,
解得S=6.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(k﹣2)x﹣3k2+12.
(1)k为何值时,图象经过原点;
(2)k为何值时,图象与直线y=﹣2x+9的交点在y轴上;
(3)k为何值时,图象平行于y=﹣2x的图象;
(4)k为何值时,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小辉从家(点0)出发,沿着等腰三角形A0B的边0A-AB-B0的路径去匀匀速散步,其中0A=0B。设小辉距家(点0)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
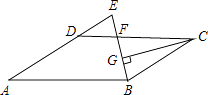
查看答案和解析>>【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A.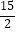
B.4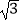
C.2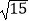
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且∠CBA=45° 求直线BC的解析式.
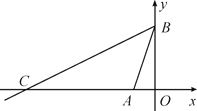
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
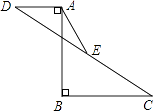
A.6
B.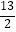
C.5
D.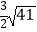
相关试题

