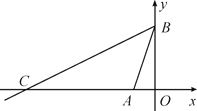
【题目】如图,在平面直角坐标系中,点A(-1,0),B(0,3),直线BC交坐标轴于B,C两点,且∠CBA=45° 求直线BC的解析式.
参考答案:
【答案】直线BC的解析式为y=![]() x+3.
x+3.
【解析】作AD⊥BC于D,
∵点A(-1,0),B(0,3),
∴OA=1,OB=3,
∴AB= ![]()
∵∠CBA=45°,
∴△ABD是等腰直角三角形,
∴BD=AD=
|
AB2
=
5 |
,
设AC=x,则OC=x+1,
∴DC=
x25 |
,
∴BC=
x25 |
+
5 |
,
在RT△OBC中,OC2+OB2=BC2,即(x+1)2+32=(
x25 |
+
5 |
),
解得x1=-
5 |
2 |
(舍去),x2=5,
∴AC=5,OC=6,
∴C(-6,0),
设直线BC的解析式为y=kx+b,
∴-6k+b=0,b=3,解得![]()
∴直线BC的解析式为y=![]() x+3.
x+3.
-
科目: 来源: 题型:
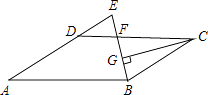
查看答案和解析>>【题目】如图,在ABCD中,AB=12,AD=8,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=2,则线段CG的长为( )
A.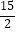
B.4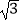
C.2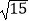
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )
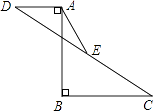
A.6
B.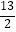
C.5
D.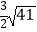
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
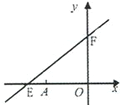
查看答案和解析>>【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
相关试题

