【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.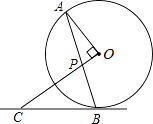
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为 ![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
参考答案:
【答案】
(1)证明:连接OB,如图,
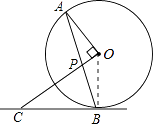
∵OP⊥OA,
∴∠AOP=90°,
∴∠A+∠APO=90°,
∵CP=CB,
∴∠CBP=∠CPB,
而∠CPB=∠APO,
∴∠APO=∠CBP,
∵OA=OB,
∴∠A=∠OBA,
∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB= ![]() ,OC=CP+OP=x+1,
,OC=CP+OP=x+1,
∵OB2+BC2=OC2,
∴( ![]() )2+x2=(x+1)2,
)2+x2=(x+1)2,
解得x=2,
即BC的长为2.
【解析】(1)首先依据垂直的定义可证明∠A+∠APO=90°,然后根据等腰三角形的性质可证明∠CBP=∠CPB,接下来,再依据根据对顶角相等得∠CPB=∠APO,然后可证明∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,最后,依据切线的判定定理进行证明即可;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理列方程求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 ,
,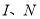 分别在
分别在 上,试说明∠MEN=∠INC+∠IME.
上,试说明∠MEN=∠INC+∠IME.(2)如图2,在(1)的条件下,若
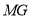 平分
平分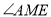 ,在
,在 上有一点
上有一点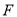 ,连接
,连接 ,使
,使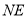 恰好平分
恰好平分 ,
, ,且
,且 的补角比
的补角比 的3倍多
的3倍多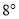 ,求
,求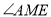 的度数;
的度数;(3)如图3,在问题(1)(2)的条件下,若点
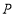 是
是 上一动点(不包含点
上一动点(不包含点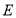 和点
和点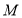 ),连接
),连接 .
.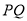 平分
平分 ,
,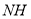 平分
平分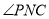 ,过
,过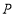 作
作 ,当点
,当点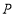 在线段
在线段 上运动时,下列结论:①
上运动时,下列结论:①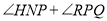 的值不变;②
的值不变;②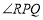 的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.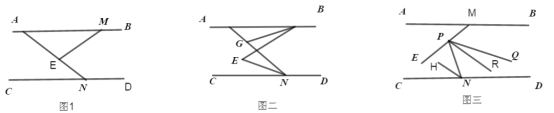
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或
C.1或
D. 或
或 
-
科目: 来源: 题型:
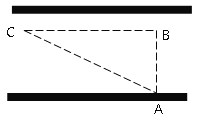
查看答案和解析>>【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图: 下面是一道证明题,刘老师给同学们讲解了思路,请将证明过程和每一步的理由补充完整.
已知:∠A=∠E,AD∥BE,求证:∠1=∠2
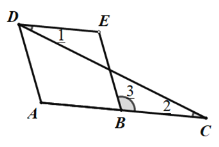
证明:
 AD∥BE(已知)
AD∥BE(已知)∠A= ( )
 ∠A=∠E ( 已知 )
∠A=∠E ( 已知 ) ∠E= (等量代换)
∠E= (等量代换) DE∥AC( )
DE∥AC( ) ∠1=∠2( )
∠1=∠2( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )
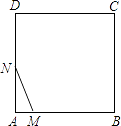
A.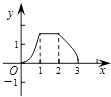
B.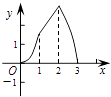
C.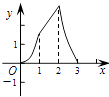
D.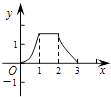
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
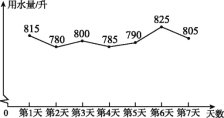

(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
相关试题

