【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或 ![]()
C.1或 ![]()
D.![]() 或
或 ![]()
参考答案:
【答案】D
【解析】解:①如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
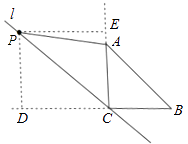
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴AB= ![]() =
= ![]() ,
,
∴AP= ![]() ;
;
∴在直角△AEP中,(1+EC)2+EP2=AP2
∴(1+DP)2+DP2=( ![]() )2,
)2,
解DP= ![]() ;
;
②如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
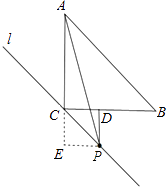
同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC﹣1)2+EP2=AP2,
∴(PD﹣1)2+PD2=( ![]() )2,
)2,
解得,PD= ![]() ;
;
所以答案是:D.
【考点精析】通过灵活运用等腰直角三角形和平行线之间的距离,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离即可以解答此题.
-
科目: 来源: 题型:
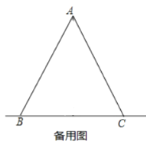
查看答案和解析>>【题目】如图,在
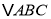 中,
中,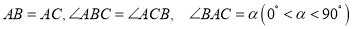 ,
,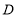 为直线
为直线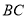 上一动点(不与点
上一动点(不与点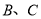 重合),在
重合),在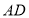 的右侧作
的右侧作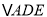 ,使得
,使得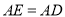 ,
,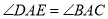 ,连接
,连接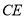 .
.(1)当点
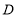 在线段
在线段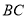 上时,求证:
上时,求证: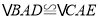 ;
;(2)当
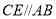 时,若点
时,若点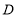 在线段
在线段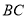 上,
上,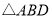 中最小角为
中最小角为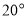 ,请求出
,请求出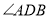 的度数;
的度数;(3)在点
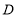 的运动过程中,当
的运动过程中,当 垂直于
垂直于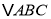 的某边时,求
的某边时,求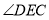 的度数(用含
的度数(用含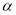 的代数式表示).
的代数式表示).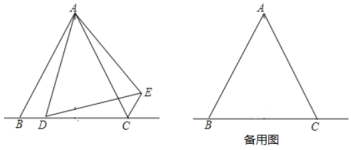
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量
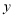 (升)与行驶时间
(升)与行驶时间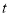 (小时)的关系如下表,请根据表格回答下列问题:
(小时)的关系如下表,请根据表格回答下列问题:时间/小时
0
1
2
3
4
5
邮箱剩余油量/升
50
45
40
35
30
25
(1)汽车行驶前油箱里有_____________升汽油,汽车每小时耗油____________升;
(2)请写出
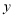 与
与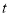 的关系式;
的关系式;(3)当汽车行驶24小时时,油箱中还剩余多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 ,
,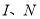 分别在
分别在 上,试说明∠MEN=∠INC+∠IME.
上,试说明∠MEN=∠INC+∠IME.(2)如图2,在(1)的条件下,若
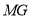 平分
平分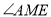 ,在
,在 上有一点
上有一点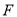 ,连接
,连接 ,使
,使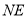 恰好平分
恰好平分 ,
, ,且
,且 的补角比
的补角比 的3倍多
的3倍多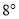 ,求
,求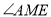 的度数;
的度数;(3)如图3,在问题(1)(2)的条件下,若点
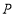 是
是 上一动点(不包含点
上一动点(不包含点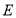 和点
和点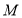 ),连接
),连接 .
.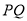 平分
平分 ,
,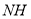 平分
平分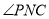 ,过
,过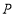 作
作 ,当点
,当点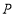 在线段
在线段 上运动时,下列结论:①
上运动时,下列结论:①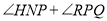 的值不变;②
的值不变;②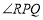 的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.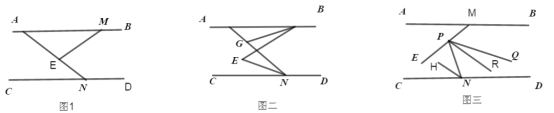
-
科目: 来源: 题型:
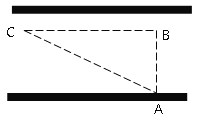
查看答案和解析>>【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
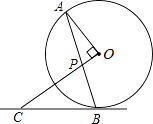
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为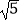 ,OP=1,求BC的长.
,OP=1,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图: 下面是一道证明题,刘老师给同学们讲解了思路,请将证明过程和每一步的理由补充完整.
已知:∠A=∠E,AD∥BE,求证:∠1=∠2
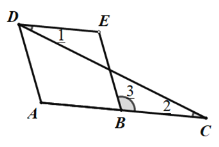
证明:
 AD∥BE(已知)
AD∥BE(已知)∠A= ( )
 ∠A=∠E ( 已知 )
∠A=∠E ( 已知 ) ∠E= (等量代换)
∠E= (等量代换) DE∥AC( )
DE∥AC( ) ∠1=∠2( )
∠1=∠2( )
相关试题

